若方程x2-mnx+m+n=0有整数根,且m、n为正整数,则m•n的值有( )
A.1个
B.3个
C.5个
D.无数个
【答案】
分析:设方程两整数根为x
1,x
2,则x
1+x
2=mn>0,x
1•x
2=m+n>0,再根据(x
1-1)(x
2-1)+(m-1)(n-1)=2,即可进行求解.
解答:解:设方程有整数根,则x
1+x
2=mn>0,x
1•x
2=m+n>0,故这两个根均为正数.
又(x
1-1)(x
2-1)+(m-1)(n-1)=2,
其中(x
1-1)(x
2-1),m-1,n-1均非负,而为两个非负整数和的情况仅有0+2;1+1;2+0.
分别可解得

,
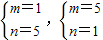
,
∴m•n的值仅有3个,
故选B.
点评:本题考查了根与系数关系,难度适中,主要掌握x
1,x
2是方程x
2+px+q=0的两根时,x
1+x
2=-p,x
1x
2=q.

 ,
,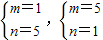 ,
,

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案