
 .
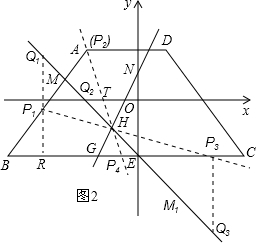
. 秒时,点G停止运动,此时直线GH与y轴交于点N.另一动点P开始从B出发,以1个单位/秒的速度沿着梯形的各边运动一周,即由B到A,然后由A到D,再由D到C,最后由C回到B(点P可以与梯形的各顶点重合).设动点P的运动时间为t秒,点M为直线HE上任意一点(点M不与点H重合),在点P的整个运动过程中,求出所有能使∠PHM与∠HNE相等的t的值.
秒时,点G停止运动,此时直线GH与y轴交于点N.另一动点P开始从B出发,以1个单位/秒的速度沿着梯形的各边运动一周,即由B到A,然后由A到D,再由D到C,最后由C回到B(点P可以与梯形的各顶点重合).设动点P的运动时间为t秒,点M为直线HE上任意一点(点M不与点H重合),在点P的整个运动过程中,求出所有能使∠PHM与∠HNE相等的t的值.
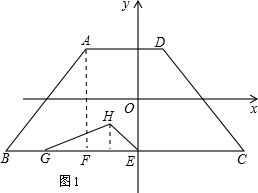 解:(1)如图1,过A作AF⊥BC.
解:(1)如图1,过A作AF⊥BC. ,∴BF=3.
,∴BF=3.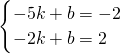 ,∴
,∴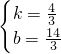 ,
,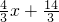 .
.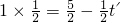 ;
;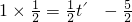 ;
; 当t′=
当t′= 秒时,GE=5-
秒时,GE=5-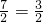
 ,-2),直线GH解析式为y=2x+1.
,-2),直线GH解析式为y=2x+1. ,可得BR=
,可得BR=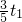 ,P1R=
,P1R=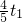 ,
,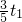 ,
,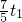 .
.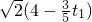 .
.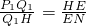 ,
, .
. 时,∠P1HM=∠HNE;
时,∠P1HM=∠HNE;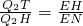 解得
解得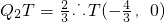 .
. .∴t4=
.∴t4=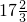
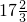 秒时,∠P4HM2=∠HNE.
秒时,∠P4HM2=∠HNE. 秒或t=5秒或t=15秒或t=
秒或t=5秒或t=15秒或t=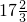 秒时,∠PHM=∠HNE.
秒时,∠PHM=∠HNE. ;
;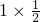 ,分别求出自变量的取值范围即可.
,分别求出自变量的取值范围即可.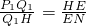 ,然后求出t1的值;
,然后求出t1的值;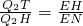 解得Q2T的长以及点T的坐标.求出直线HT的解析式后求出t2的值;
解得Q2T的长以及点T的坐标.求出直线HT的解析式后求出t2的值;

科目:初中数学 来源: 题型:
| 4 | 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 5 |
| 7 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2011年湖北省鄂州市石山中学中考数学模拟试卷(五)(解析版) 题型:解答题
 .
. 秒时,点G停止运动,此时直线GH与y轴交于点N.另一动点P开始从B出发,以1个单位/秒的速度沿着梯形的各边运动一周,即由B到A,然后由A到D,再由D到C,最后由C回到B(点P可以与梯形的各顶点重合).设动点P的运动时间为t秒,点M为直线HE上任意一点(点M不与点H重合),在点P的整个运动过程中,求出所有能使∠PHM与∠HNE相等的t的值.
秒时,点G停止运动,此时直线GH与y轴交于点N.另一动点P开始从B出发,以1个单位/秒的速度沿着梯形的各边运动一周,即由B到A,然后由A到D,再由D到C,最后由C回到B(点P可以与梯形的各顶点重合).设动点P的运动时间为t秒,点M为直线HE上任意一点(点M不与点H重合),在点P的整个运动过程中,求出所有能使∠PHM与∠HNE相等的t的值.
查看答案和解析>>
科目:初中数学 来源:2007年黑龙江省哈尔滨市中考数学试卷(解析版) 题型:解答题
 .
. 秒时,点G停止运动,此时直线GH与y轴交于点N.另一动点P开始从B出发,以1个单位/秒的速度沿着梯形的各边运动一周,即由B到A,然后由A到D,再由D到C,最后由C回到B(点P可以与梯形的各顶点重合).设动点P的运动时间为t秒,点M为直线HE上任意一点(点M不与点H重合),在点P的整个运动过程中,求出所有能使∠PHM与∠HNE相等的t的值.
秒时,点G停止运动,此时直线GH与y轴交于点N.另一动点P开始从B出发,以1个单位/秒的速度沿着梯形的各边运动一周,即由B到A,然后由A到D,再由D到C,最后由C回到B(点P可以与梯形的各顶点重合).设动点P的运动时间为t秒,点M为直线HE上任意一点(点M不与点H重合),在点P的整个运动过程中,求出所有能使∠PHM与∠HNE相等的t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com