
【题目】如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点M距水面6米(即MO=6米),小孔顶点N距水面4.5米(即NC=4.5米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度EF.

【答案】10米.
【解析】
试题分析:考查二次函数的性质与实际运用能力.建立函数模型的关键是准确找出模型类型,然后利用待定系数法求出模型(即函数)的表达式,最后根据函数的性质得出结论.根据图形很容易可以知道这是由三条抛物线组成的,观察图象可知抛物线的对称轴为y轴,顶点为(0,6),故设解析式为y=ax2+6,又因为AB=20,所以OB=10,故B(10,0)在抛物线上,代入解析式可求得a=﹣0.06.第(2)问中当水位上涨到刚好淹没小孔时,OD=4.5,即E、F两点纵坐标为4.5,代入解析式求出E或F点横坐标即可.
试题解析:
解:设抛物线解析式为y=ax2+6,(1分)
依题意得,B(10,0).
∴a×102+6=0,
解得:a=﹣0.06,
即y=﹣0.06x2+6.(4分)
当y=4.5时,﹣0.06x2+6=4.5,
解得x=±5,
∴DF=5,EF=10,
即水面宽度为10米.(8分)


科目:初中数学 来源: 题型:
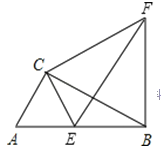
【题目】如图:在△ABC中,∠ACB=90°,∠ABC=30°,AC=1,现将△ABC绕点C逆时针旋转至△EFC,使点E恰巧落在AB上,连接BF,则BF的长度为( )
A、![]() B、2 C、1 D、
B、2 C、1 D、![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b是有理数,那么下列结论一定正确的是()
A. 若a<b,则│a│<│b│ B. 若a>b,则│a│>│b│
C. 若a=b,则│a│=│b│ D. 若a≠b,则│a│≠│b│
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为元时,该服装店平均每天的销售利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把a3-ab2分解因式的正确结果是( )
A. (a+ab)(a-ab)B. a(a2-b2)
C. a(a+b)(a-b)D. a(a-b)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com