有一人患了流感,经过两轮传染后共有144人患了流感,问:
(1)每轮传染中平均一个人传染了几个人?
(2)按照这样的速度,三轮传染后有多少人患流感?
(3)设前n轮传染的平均数为S1,前n-1轮传染的平均数为S2,是否存在一个正整数K,使S1=KS2?若存在求出所有K的值;若不存在,请说明理由.
解:(1)设每轮传染中平均一个人传染了x个人,依题意得1+x+x(1+x)=144,即(1+x)
2=144
解方程得x
1=11,x
2=-13(舍去)
答:每轮传染中平均一人传染了11人.
(2)经过三轮传染后患上流感的人数为:144+11×144=1728(人),
答:经过三轮传染后患上流感的人数为1728人.
(3)
∵根据题意得:第一轮有12=12
1人患感冒,
第二轮有144=12
2人患感冒,
第三轮有1728=12
3人患感冒,
…
∴第n轮共有12
n人患感冒,第n-1轮共有12
n-1人患感冒,
∴S
1=

,
S
2=
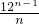
∴k=

=

=12,
∴在一个正整数k=12,使S
1=KS
2.
分析:(1)患流感的人把病毒传染给别人,自己仍然患病,包括在总数中.设每轮传染中平均一个人传染了x个人,则第一轮传染了x个人,第二轮作为传染源的是(x+1)人,则传染x(x+1)人,依题意列方程:1+x+x(1+x)=144,解方程即可求解.
(2)根据(1)中所求数据,进而表示出经过三轮传染后患上流感的人数.
(3)设存在正整数k,然后分别表示出S
1和S
2,然后求得其比值为正整数即可解答.
点评:本题考查了一元二次方程的应用,关键是看到两轮传染,从而可列方程求解.

 ,
,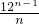
 =
= =12,
=12,
