
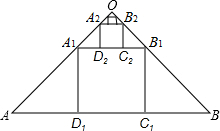
 如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中作内接正方形A3B3C3D3;…;依次作下去,则第2016个正方形A2016B2016C2016D2016的边长是$(\frac{1}{3})^{2016}$.
如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中作内接正方形A3B3C3D3;…;依次作下去,则第2016个正方形A2016B2016C2016D2016的边长是$(\frac{1}{3})^{2016}$. 分析 根据等腰直角三角形和正方形的性质可以得出AnDn+1=Dn+1Cn+1=Cn+1Bn=$\frac{1}{3}$AnBn,再结合AB=1即可得出AnBn=$(\frac{1}{3})^{n}$,代入n=2016即可得出结论.
解答 解:∵△OAnBn为等腰直角三角形,
∴AnDn+1=Dn+1Cn+1=Cn+1Bn=$\frac{1}{3}$AnBn,
∵AB=1,
∴AnBn=$(\frac{1}{3})^{n}$,
∴第2016个正方形A2016B2016C2016D2016的边长是$(\frac{1}{3})^{2016}$.
故答案为:$(\frac{1}{3})^{2016}$.
点评 本题考查了正方形的性质以及等腰直角三角形的性质,解题的关键是找出AnBn=$(\frac{1}{3})^{n}$.本题属于基础题,难度不大,解决该题型题目时,根据正方形和等腰直角三角形的性质找出正方形的边长通式是关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABC和∠BAC的角平分线交于点O,OD⊥BC,OE⊥AC,OF⊥AB,垂足分别为D、E、F. OC平分∠ACB吗?为什么?
如图,在△ABC中,∠ABC和∠BAC的角平分线交于点O,OD⊥BC,OE⊥AC,OF⊥AB,垂足分别为D、E、F. OC平分∠ACB吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com