
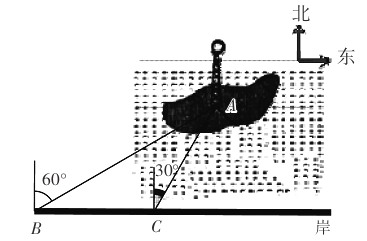
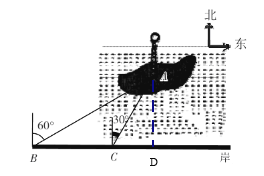
【题目】如图,郴州北湖公园的小岛上有为了纪念唐代著名诗人韩愈而建的韩愈铜像,其底部为A.某人在岸边的B处测得A在B的北偏东60°的方向上.然后沿岸边直行200米到达C处,再次测得A在C的北偏东30°的方向上(其中A,B,C在同一平面上).求这个铜像底部A到岸边BC的距离(结果精确到0.1米,参考数据:![]() ≈1.732)
≈1.732)
【答案】173.2米
【解析】
试题分析:作AD⊥BC延长线于点D,根据条件给出角的度数能推出△ABC为等腰三角形,可得出AC=AB=200,根据Rt△ACD中∠ACD的正弦值得出AD=AC·sin∠ACD≈173.2米.
试题解析:过点A作AD⊥BC于D,则AD的长度就是A到岸边BC的距离. ∵依题意可知∠ABC=90°-60°=30°,∠ACD=90°-30°=60°∴∠BAC=60°-30°=30°,∴∠ABC=∠BAC ∴AC=BC=200,∵在Rt△ACD中,sin∠ACD=![]() ∴sin60°=
∴sin60°=![]() ,∴AD=200sin60°=
,∴AD=200sin60°=![]() ≈173.2米
≈173.2米
答:这个铜像底部A到岸边BC的最短距离为173.2米.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】某课外兴趣小组为了解所在地区老年人的健康状况,分别作了四种不同的抽样调查.你认为抽样比较合理的是( )
A.在公园调查了1000名老年人的健康状况
B.在医院调查了1000名老年人的健康状况
C.调查了10名老年邻居的健康状况
D.利用派出所的户籍网随机调查了该地区10%的老年人的健康状况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在市委宣传部举办的以“弘扬社会主义核心价值观”为主题的演讲比赛中,其中10位参赛选手的成绩如下:9.3;9.5;8.9;9.3;9.5;9.5;9.7;9.4;9.5,这组数据的众数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
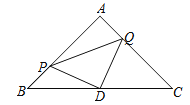
【题目】如图,△ABC是等腰直角三角形,∠A=90o,点P、Q分别是AB、AC上的动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com