
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
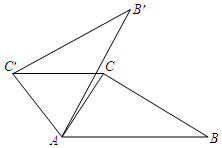 如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等腰△ABC中,AB=AC=5,半径为1的⊙O分别与AB、AC相切于E、F两点,BG是⊙O的切线,切点为G,则BG的长为$\frac{11}{3}$.
如图,在等腰△ABC中,AB=AC=5,半径为1的⊙O分别与AB、AC相切于E、F两点,BG是⊙O的切线,切点为G,则BG的长为$\frac{11}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
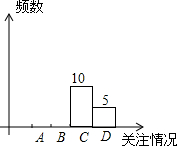 2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.
2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.| 关注情况 | 频数 | 频率 |
| A.高度关注 | k | 0.2 |
| B.一般关注 | m | 0.5 |
| C.极少关注 | 10 | n |
| D.不关注 | 5 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com