
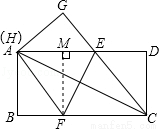
(2014•德州)如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2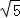 .
.
以上结论中,你认为正确的有( )个.

A.1 B.2 C.3 D.4
C
【解析】
试题分析:先判断出四边形CFHE是平行四边形,再根据翻折的性质可得CF=FH,然后根据邻边相等的平行四边形是菱形证明,判断出①正确;
根据菱形的对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时EC平分∠DCH,判断出②错误;
点H与点A重合时,设BF=x,表示出AF=FC=8﹣x,利用勾股定理列出方程求解得到BF的最小值,点G与点D重合时,CF=CD,求出BF=4,然后写出BF的取值范围,判断出③正确;
过点F作FM⊥AD于M,求出ME,再利用勾股定理列式求解得到EF,判断出④正确.
【解析】
∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四边形CFHE是平行四边形,
由翻折的性质得,CF=FH,
∴四边形CFHE是菱形,(故①正确);
∴∠BCH=∠ECH,
∴只有∠DCE=30°时EC平分∠DCH,(故②错误);
点H与点A重合时,设BF=x,则AF=FC=8﹣x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8﹣x)2,
解得x=3,
点G与点D重合时,CF=CD=4,
∴BF=4,
∴线段BF的取值范围为3≤BF≤4,(故③正确);
过点F作FM⊥AD于M,
则ME=(8﹣3)﹣3=2,
由勾股定理得,
EF=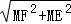 =
=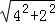 =2
=2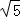 ,(故④正确);
,(故④正确);
综上所述,结论正确的有①③④共3个.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:[同步]2014年人教版初中数学九年级上第二十二章22.2练习卷(解析版) 题型:选择题
(2014•宜宾)若关于x的一元二次方程的两个根为x1=1,x2=2,则这个方程是( )
A.x2+3x﹣2=0 B.x2﹣3x+2=0 C.x2﹣2x+3=0 D.x2+3x+2=0
查看答案和解析>>
科目:初中数学 来源:[同步]2014年人教版初中数学九年级上第二十二章22.3练习卷(解析版) 题型:
(2014•中江县一模)到2013底,我县已建立了比较完善的经济困难学生资助体系.某校2011年发放给每个经济困难学生450元,2013年发放的金额为625元.设每年发放的资助金额的平均增长率为x,则下面列出的方程中正确的是( )
A.450(1+x)2=625 B.450(1+x)=625 C.450(1+2x)=625 D.625(1+x)2=450
查看答案和解析>>
科目:初中数学 来源:[同步]2014年人教版初中数学八年级上第十三章13.4练习卷(解析版) 题型:选择题
(2014•牡丹江)已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( )

A.30° B.40° C.50° D.60°
查看答案和解析>>
科目:初中数学 来源:[同步]2014年人教版初中数学八年级上第十三章13.4练习卷(解析版) 题型:选择题
(2014•潍坊)如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
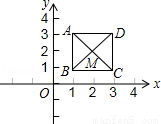
A.(﹣2012,2) B.(﹣2012,﹣2) C.(﹣2013,﹣2) D.(﹣2013,2)
查看答案和解析>>
科目:初中数学 来源:[同步]2014年人教版初中数学九年级下第二十九章29.3练习卷(解析版) 题型:选择题
(2014•沈阳)某几何体的三视图如图所示,这个几何体是( )

A.圆柱 B.三棱柱 C.长方体 D.圆锥
查看答案和解析>>
科目:初中数学 来源:[同步]2014年人教版初中数学九年级下第二十九章29.3练习卷(解析版) 题型:选择题
(2014•张家界)某几何体的主视图、左视图和俯视图分别如图所示,则该几何体的体积为( )
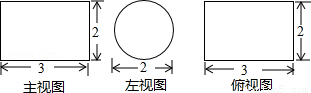
A.3π B.2π C.π D.12
查看答案和解析>>
科目:初中数学 来源:[同步]2014年北师大版初中数学七年级上第四章4.1练习卷(解析版) 题型:选择题
(2012•高州市一模)下列说法错误的是( )
A.两点确定一条直线 B.线段是直线的一部分
C.一条直线是一个平角 D.把线段向两边延长即是直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com