
分析 (1)根据提公因式法可以解答此方程;
(2)根据二次根式的混合运算的方法可以解答本题.
解答 解:(1)x2=3x
x2-3x=0,
x(x-3)=0,
∴x=0或x-3=0,
解得,x1=0,x2=3;
(2)$\sqrt{18}$-4$\sqrt{\frac{1}{2}}$+$\sqrt{24}$÷$\sqrt{3}$
=3$\sqrt{2}$-2$\sqrt{2}$+$2\sqrt{6}÷\sqrt{3}$
=3$\sqrt{2}$-2$\sqrt{2}$+$2\sqrt{2}$
=$3\sqrt{2}$.
点评 本题考查二次根式的混合运算、解一元二次方程-因式分解法,解题的关键的关键明确它们各自的解答方法.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一斜坡上栽树,相邻在坡面上的距离AB=13m,水平距离为12m,则该斜坡坡度i为( )
如图,一斜坡上栽树,相邻在坡面上的距离AB=13m,水平距离为12m,则该斜坡坡度i为( )| A. | 5:12 | B. | 12:13 | C. | 12:5 | D. | 1:$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
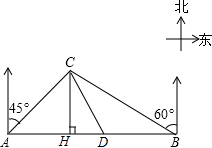 川西某高原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
川西某高原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com