
分析 设B(x0,y0),则C($\frac{1}{{x}_{0}}$,$\frac{1}{{y}_{0}}$),根据等边三角形性质得到(x0+1)2+(y0+1)2=(x0-$\frac{1}{{x}_{0}}$)2+(y0-$\frac{1}{{y}_{0}}$)2,解方程即可得到结论.
解答 解:设B(x0,y0),则C($\frac{1}{{x}_{0}}$,$\frac{1}{{y}_{0}}$),
∵△ABC是等边三角形,
∴AB=AC,
∴(x0+1)2+(y0+1)2=(x0-$\frac{1}{{x}_{0}}$)2+(y0-$\frac{1}{{y}_{0}}$)2,
∵y0=$\frac{1}{{x}_{0}}$,
∴($\frac{1}{{x}_{0}}$+x0)2-2($\frac{1}{{x}_{0}}$+x0)-9=0,
∴$\frac{1}{{x}_{0}}$+x0=4,或-2(舍去),
∴x0=2±$\sqrt{3}$,y0=2±$\sqrt{3}$,
∴B(2-$\sqrt{3}$,2+$\sqrt{3}$),C(2+$\sqrt{3}$,2-$\sqrt{3}$),∴BC=2$\sqrt{6}$.
∴△ABC的边长等于2$\sqrt{6}$.
故答案为:2$\sqrt{6}$.
点评 本题考查了反比例函数图形上点的坐标特征,熟记反比例函数的性质是解题的关键.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
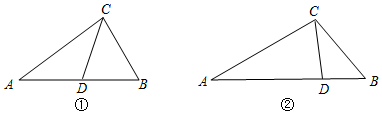
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
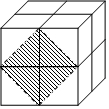 如图,这是由8个同样大小的立方体组成的魔方,体积为8cm3.
如图,这是由8个同样大小的立方体组成的魔方,体积为8cm3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
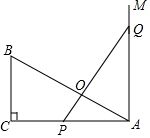 如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.
如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +1 | +1.2 | -1 | +2 | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com