
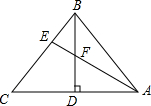
 (2012•南岗区二模)已知:BD为△ABC边AC上的高,E为BC上一点,CE=2BE,∠CAE=30°,若EF=3,BF=4,则AF的长为
(2012•南岗区二模)已知:BD为△ABC边AC上的高,E为BC上一点,CE=2BE,∠CAE=30°,若EF=3,BF=4,则AF的长为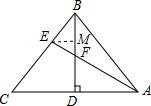 过E作EM⊥BD于M,则∠BME=∠FME=90°,
过E作EM⊥BD于M,则∠BME=∠FME=90°,| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 5 |
| 2 |
| BM2+EM2 |
| 13 |
| 13 |
| BD |
| BC |
| BM |
| BE |
| ||
|
| BD | ||
3
|
| ||
|
| 15 |
| 2 |
| 15 |
| 2 |
| 7 |
| 2 |


 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
 (2012•南岗区二模)如图,在Rt△ABC中.∠C=90°,BC=6,AC=8,点D在AC上,将△BCD沿BD折叠,使点C恰好落在AB边的点C′处,则△ADC′的面积是( )
(2012•南岗区二模)如图,在Rt△ABC中.∠C=90°,BC=6,AC=8,点D在AC上,将△BCD沿BD折叠,使点C恰好落在AB边的点C′处,则△ADC′的面积是( )查看答案和解析>>
科目:初中数学 来源: 题型:
(2012•南岗区二模)下列表格列出了一项实验的统计数据,它表示皮球从一定高度落下时,下落高度y与弹跳高度x的关系,能表示这种关系的函数关系式为( )
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com