在四边形ABCD中,AC⊥BD,AB=AD,要使四边形ABCD是菱形,只需添加一个条件,这个条件可以是________(只要填写一种情况).
AB∥CD(本题答案不唯一)
分析:首先根据条件可得∠AOD=∠AOB=90°,再证明Rt△ABO≌Rt△ADO,从而得到BO=DO,再证明△ABO≌Rt△CDO,进而得到AB=CD,再加上条件AB∥CD可得到四边形ABCD是平行四边形,又有AB=AD可证出四边形ABCD是菱形.
解答:添加条件AB∥CD,
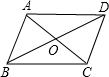
理由:∵AC⊥BD,
∴∠AOD=∠AOB=90°,
在Rt△ABO和Rt△ADO中
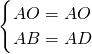
,
∴Rt△ABO≌Rt△ADO,
∴BO=DO,
∵AB∥CD,
∴∠ABO=∠CDO,
在△ABO和Rt△CDO中
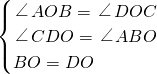
,
∴△ABO≌Rt△CDO,
∴AB=CD,
∴四边形ABCD是平行四边形,
又∵AB=AD,
∴四边形ABCD是菱形.
点评:此题主要考查了全等三角形的判定,平行四边形的判定,菱形的判定,解决问题的关键是证明AB=CD,从而得到四边形ABCD是平行四边形.


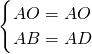 ,
,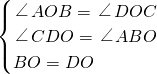 ,
,
