
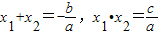 .我们把它们称为根与系数关系定理.
.我们把它们称为根与系数关系定理.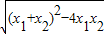 =
=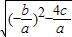 =
=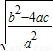 =
=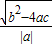
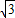 AB=2CD.
AB=2CD.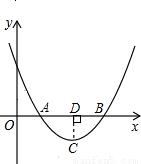 解:(1)当△ABC为等腰直角三角形时,过C作CD⊥AB于D,则AB=2CD;
解:(1)当△ABC为等腰直角三角形时,过C作CD⊥AB于D,则AB=2CD;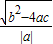 ,
,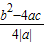 ,a≠0,
,a≠0,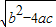 =
=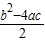 ,
,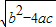 =
=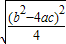 ,
,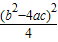 ,
,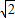 ;
;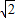 x+1向上或向下平移使∠ACB=60°,然后向左或向右平移任意个单位即可.
x+1向上或向下平移使∠ACB=60°,然后向左或向右平移任意个单位即可. x+1+m,
x+1+m,

 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源:2010年北京市大兴区中考数学一模试卷(解析版) 题型:解答题
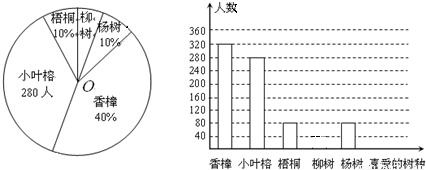
查看答案和解析>>
科目:初中数学 来源:2010年北京市大兴区中考数学一模试卷(解析版) 题型:填空题
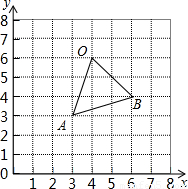
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com