
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.

(1)求证:AD=EC;
(2)当点D是BC的中点时,求证:四边形ADCE是矩形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)利用SAS证得△ACD≌△ECD后即可证得AD=EC;
(2)当点D是BC中点时,四边形ADCE是矩形;首先证得四边形ADCE是平行四边形,然后证得AD⊥BC即可利用有一个角是直角的平行四边形是矩形判定矩形.
试题解析:
(1)由平移可得:AB∥DE,AB=DE
∴∠B=∠EDC
∵AB=AC
∴∠B=∠ACD,AC=DE
∴∠EDC=∠ACD
又∵DC=CD
∴△ACD≌△EDC(SAS)
∴AD=EC
(2)∵AB=AC,点D是BC的中点
∴BD=DC,AD⊥BC
由平移的性质可知AE∥BD,可得四边形ABDE是平行四边形
∴AE=BD,AE∥BD
∴AE=DC,AE∥DC
∴四边形ADCE是平行四边形
∵AD⊥BC
∴平行四边形ADCE是矩形


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(本题满分8分)东台沿海高速公路养护小组,乘车沿南北向公路巡视维护,如果约定向北为正,向南为负, 当天的行驶记录如下:(单位:km)
+17,-9,+7,-15,-3,+11,-6,-8,+5,+16
(1) 养护小组最后到达的地方在出发点的哪个方向?距出发点多远?
(2) 养护过程中,最远处离出发点有多远?
(3) 若汽车耗油为0.5L/km,则这次养护共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l与坐标轴相交于点M(3,0),N(0,﹣4),反比例函数y=![]() (x>0)的图象经过Rt△MON的外心A.
(x>0)的图象经过Rt△MON的外心A.

(1)求直线l的解析式;
(2)直接写出点A坐标及k值;
(3)在函数y=![]() (x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P,若△OMP的面积与△OBC的面积相等,求点P的坐标.
(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P,若△OMP的面积与△OBC的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
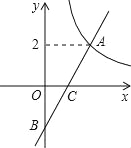
【题目】如图在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与一次函数y=kx-k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx-k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx-k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com