解:(1)原不等式可化为(m+3)x>3-3m,
当m+3>0,即m>-3时,原不等式的解集为:x>
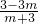
;
当m+3<0,即m<-3时,原不等式的解集为:x<
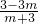
;
当m+3=0,即m=-3时,原不等式可化为0>3-3m=12,原不等式无解.
(2)原不等式可化为ax>2b的形式,
当a>0时,原不等式的解集为x>
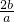
;
当a<0时,原不等式的解集为x<
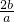
;
当a=0时,原不等式可化为0>2b,当b<0时不等式的解集为全体实数,当b≥0时,不等式无解.
(3)原不等式组可化为
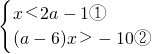
,
当a-6>0,即a>6时,不等式②的解集为x>-
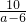
,显然原不等式组的解集为-
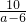
<x<2a-1;
当a-6<0,即a<6时,不等式②的解集为x<-
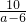
,当-
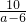
<2a-1时,原不等式组的解集为-
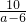
<x<2a-1,当-
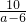
≥2a-1时,原不等式组无解.
分析:(1)先把原不等式去分母、去括号、移项、合并同类项化为(m+3)x>3-3m的形式,再分m+3>0,
m+3<0,m+3=0三种情况讨论不等式的解集;
(2)先把原不等式化为ax>2b的形式,再分a>0,a<0,a=0三种情况讨论x的取值范围;
(3)先把原不等式组化为
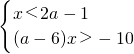
的形式,再根据a-6的符号求出x的取值范围.
点评:本题考查的是一元一次不等式及一元一次不等式组的解法,解答此类问题时一定要分类讨论,否则会造成漏解.

 mx-1>-[x(m+1)+m]
mx-1>-[x(m+1)+m] .
.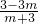 ;
;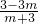 ;
;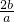 ;
;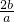 ;
;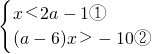 ,
,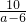 ,显然原不等式组的解集为-
,显然原不等式组的解集为-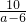 <x<2a-1;
<x<2a-1;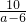 ,当-
,当-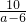 <2a-1时,原不等式组的解集为-
<2a-1时,原不等式组的解集为-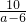 <x<2a-1,当-
<x<2a-1,当-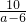 ≥2a-1时,原不等式组无解.
≥2a-1时,原不等式组无解.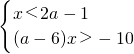 的形式,再根据a-6的符号求出x的取值范围.
的形式,再根据a-6的符号求出x的取值范围.

 阅读快车系列答案
阅读快车系列答案