
科目:初中数学 来源: 题型:解答题
 如图,以?ABCD的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$的图象交BC于D,连接AD.
如图,以?ABCD的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$的图象交BC于D,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
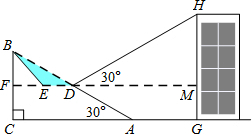 如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).
如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
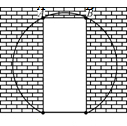 温州外国语学校在进行校园二次美化工程,一面墙上有一个矩形的门洞,如图,已知矩形的高为2米,宽为0.8米,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,圆弧所在的圆的半径长为$\frac{2\sqrt{29}}{5}$米.
温州外国语学校在进行校园二次美化工程,一面墙上有一个矩形的门洞,如图,已知矩形的高为2米,宽为0.8米,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,圆弧所在的圆的半径长为$\frac{2\sqrt{29}}{5}$米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
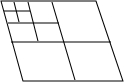 如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )
如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )| A. | 2n个 | B. | (2n+1)个 | C. | 3n个 | D. | (3n+1)个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com