
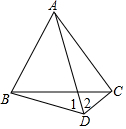
 如图,四边形ABDC中,∠BAC+∠BDC=180°.
如图,四边形ABDC中,∠BAC+∠BDC=180°.分析 (1)过点A作AE⊥BD于E,作AF⊥DC于F,先判定△ABE≌△ACF(AAS),再根据AE=AF,AE⊥BD,AF⊥DC,得出AD平分∠BDC即可;
(2)过点A作AE⊥BD于E,作AF⊥DC于F,先根据∠1=∠2,AE⊥BD,AF⊥DC,得出AE=AF,再判定△ABE≌△ACF(ASA),即可得出AB=AC;
(3)在AD上截取AG=BD,连接CG,先判定△BCD≌△ACG(SAS),得到CD=CG,再判定△DCG是等边三角形,得到DG=CD,进而得出BD+CD=AG+GD=AD.
解答 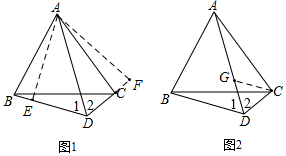 解:(1)如图1,过点A作AE⊥BD于E,作AF⊥DC于F,则∠AEB=∠F=90°,
解:(1)如图1,过点A作AE⊥BD于E,作AF⊥DC于F,则∠AEB=∠F=90°,
∴四边形AEDF中,∠EAF+∠BDC=180°,
∵∠BAC+∠BDC=180°,
∴∠EAF=∠BAC,
∴∠BAE=∠CAF,
又∵AB=AC,
∴△ABE≌△ACF(AAS),
∴AE=AF,
又∵AE⊥BD,AF⊥DC,
∴AD平分∠BDC,
即∠1=∠2;
(2)如图1,过点A作AE⊥BD于E,作AF⊥DC于F,则∠AEB=∠F=90°,
∴四边形AEDF中,∠EAF+∠BDC=180°,
∵∠BAC+∠BDC=180°,
∴∠EAF=∠BAC,
∴∠BAE=∠CAF,
∵∠1=∠2,AE⊥BD,AF⊥DC,
∴AE=AF,
∴△ABE≌△ACF(ASA),
∴AB=AC;
(3)如图2,在AD上截取AG=BD,连接CG,
∵∠BAC=60°,AB=AC,
∴△ABC是等边三角形,
∴BC=AC,∠BAC=∠ACB=60°,
∵∠BAC+∠BDC=180°,
∴∠BDC=120°,
∴由(1)可得,∠1=∠2=60°,
∴∠1=∠ACB,
∵AD与BC交于一点,
∴∠CAG=∠CBD,
∴△BCD≌△ACG(SAS),
∴CD=CG,∠ACG=∠BCD,
又∵∠ACG+∠BCG=60°,
∴∠BCD+∠BCG=60°,即∠DCG=60°,
∴△DCG是等边三角形,
∴DG=CD,
∴BD+CD=AG+GD=AD.
点评 本题主要考查了等边三角形的性质、全等三角形的判定与性质的运用,解决问题的关键是作辅助线构造全等三角形和等边三角形,根据全等三角形的对应边相等进行推导.解题时注意:等边三角形的边角性质为证明线段、角相等提供了便利条件.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:填空题
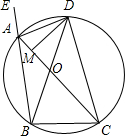 如图,△ABC内接于⊙O,其外角平分线AD交⊙O于D,DM⊥AC于M,下列结论中正确的是①②③.
如图,△ABC内接于⊙O,其外角平分线AD交⊙O于D,DM⊥AC于M,下列结论中正确的是①②③.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com