
如图,四边形ABCD中,∠BAD=∠ACB=90º,AB=AD,AC=4BC,设CD的长为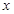 ,四边形ABCD的面积为
,四边形ABCD的面积为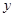 ,则
,则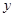 与
与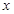 之间的函数关系式是( )
之间的函数关系式是( )

A.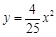 B.
B.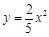
C.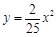 D.
D.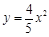
B
【解析】
试题分析:将△ABC绕点A逆时针旋转90°到△ADE的位置,根据全等三角形的性质,结合勾股定理,把梯形的上底DE,下底AC,高DF分别用含x的式子表示,即可得到结果.
如图,作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,

∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE
∴∠BAC=∠DAE
又∵AB=AD,∠ACB=∠E=90°
∴△ABC≌△ADE(AAS)
∴BC=DE,AC=AE,
设BC=a,则DE=a,DF=AE=AC=4BC=4a,
CF=AC-AF=AC-DE=3a,
在Rt△CDF中,由勾股定理得,
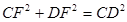 ,即
,即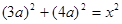 ,
,
解得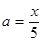
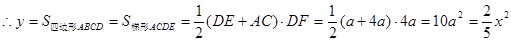
故选C.
考点:本题考查的是根据实际问题列二次函数关系式
点评:本题运用了旋转的性质,将求不规则四边形的面积问题转化为求梯形的面积,充分体现了全等三角形,勾股定理再解题中的作用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com