
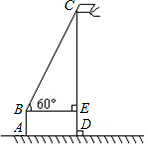
 小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 科目:初中数学 来源: 题型:解答题
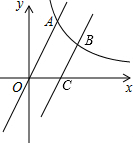 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
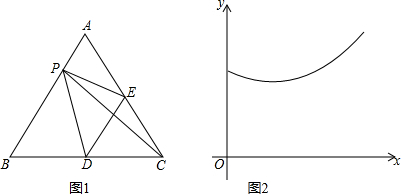
| A. | 线段PE | B. | 线段PD | C. | 线段PC | D. | 线段DE |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
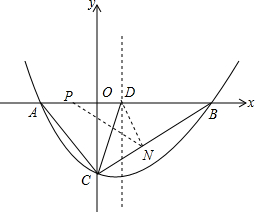 已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,-8),对称轴为x=4.
已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,-8),对称轴为x=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com