
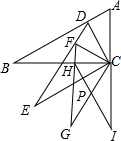
 如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长.
如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长. 分析 本题介绍两种方法:
①在Rt△ACD中,利用30度角的性质和勾股定理求CD的长;同理在Rt△ECD中求FC的长,在Rt△FCG中求CH的长;最后在Rt△HCI中,利用30度角的性质和勾股定理求CI的长.
②在Rt△DCA中,利用30°角的余弦求CD,同理依次求CF、CH、CP,最后利用正弦求CI的长.
解答 解:解法一:在Rt△ACB中,∠B=30°,∠ACB=90°,
∴∠A=90°-30°=60°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=30°,
在Rt△ACD中,AC=a,
∴AD=$\frac{1}{2}$a,
由勾股定理得:CD=$\sqrt{{a}^{2}-(\frac{1}{2}a)^{2}}$=$\frac{\sqrt{3}a}{2}$,
同理得:FC=$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}a}{2}$=$\frac{3a}{4}$,CH=$\frac{\sqrt{3}}{2}$×$\frac{3a}{4}$=$\frac{3\sqrt{3}a}{8}$,
在Rt△HCI中,∠I=30°,
∴HI=2HC=$\frac{3\sqrt{3}a}{4}$,
由勾股定理得:CI=$\sqrt{(\frac{3\sqrt{3}a}{4})^{2}-(\frac{3\sqrt{3}a}{8})^{2}}$=$\frac{9a}{8}$,
解法二:∠DCA=∠B=30°,
在Rt△DCA中,cos30°=$\frac{CD}{AC}$,
∴CD=AC•cos30°=$\frac{\sqrt{3}}{2}$a,
在Rt△CDF中,cos30°=$\frac{CF}{CD}$,
CF=$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$a=$\frac{3}{4}$a,
同理得:CH=cos30°CF=$\frac{\sqrt{3}}{2}$×$\frac{3}{4}$a=$\frac{3\sqrt{3}}{8}$a,
在Rt△HCI中,∠HIC=30°,
tan30°=$\frac{CH}{CI}$,
CI=$\frac{3\sqrt{3}}{8}$a÷$\frac{\sqrt{3}}{3}$=$\frac{9}{8}$a;
答:CI的长为$\frac{9a}{8}$.
点评 本题考查了勾股定理和直角三角形含30°角的性质,在直角三角形中,30°角所对的直角边等于斜边的一半,这一性质经常运用,必须熟练掌握;同时在运用勾股定理和直角三角形含30°角的性质时,一定要书写好所在的直角三角形,尤其是此题多次运用了这一性质,此题也可以利用三角函数解决.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{54}•\sqrt{\frac{1}{2}}=\frac{3}{2}\sqrt{6}$ | B. | $\sqrt{36}=±6$ | C. | x4+x4=2x4 | D. | (x2y)3=x6y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com