
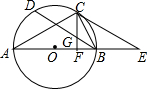
 如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.分析 (1)连接OC,先证得$\widehat{BC}$=$\widehat{DC}$,根据垂径定理得到OC⊥BD,根据CE∥BD推出OC⊥CE,即可得到结论;
(2)根据圆周角定理得出∠ACB=90°,然后根据同角的余角相等得出∠A=∠BCF,即可证得∠BCF=∠CBD,根据同角对等边即可证得结论;
(3)连接AD,根据圆周角定理得出∠ADB=90°,即可求得∠BAD=60°,根据圆周角定理得出∠DAC=∠BAC=30°,解直角三角形求得$\frac{BC}{AC}$=tan30°=$\frac{\sqrt{3}}{3}$,然后根据三角形相似和等腰三角形的判定即可求得BE的值.
解答 (1)证明:连接OC,
∵∠A=∠CBD,
∴$\widehat{BC}$=$\widehat{DC}$,
∴OC⊥BD,
∵CE∥BD,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)证明:∵AB为直径,
∴∠ACB=90°,
∵CF⊥AB,
∴∠ACB=∠CFB=90°,
∵∠ABC=∠CBF,
∴∠A=∠BCF,
∵∠A=∠CBD,
∴∠BCF=∠CBD,
∴CG=BG;
(3)解:连接AD,
∵AB为直径,
∴∠ADB=90°,
∵∠DBA=30°,
∴∠BAD=60°,
∵$\widehat{BC}$=$\widehat{DC}$,
∴∠DAC=∠BAC=$\frac{1}{2}$∠BAD=30°,
∴$\frac{BC}{AC}$=tan30°=$\frac{\sqrt{3}}{3}$,
∵CE∥BD,
∴∠E=∠DBA=30°,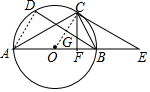
∴AC=CE,
∴$\frac{BC}{CE}$=$\frac{\sqrt{3}}{3}$,
∵∠A=∠BCF=∠CBD=30°,
∴∠BCE=30°,
∴BE=BC,
∴△CGB∽△CBE,
∴$\frac{CG}{BC}$=$\frac{BC}{CE}$=$\frac{\sqrt{3}}{3}$,
∵CG=4,
∴BC=4$\sqrt{3}$,
∴BE=4$\sqrt{3}$.
点评 本题考查了圆周角定理,垂径定理,切线的判定和性质以及三角形相似的判定和性质,作出辅助线构建直角三角形是解题的关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
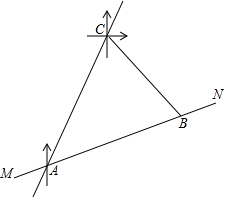 超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{7}{4}$ | C. | $\frac{8\sqrt{10}}{3}$ | D. | $\frac{28}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
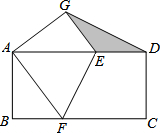 如图:矩形ABCD中,AB=4,BC=8,将矩形折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,
如图:矩形ABCD中,AB=4,BC=8,将矩形折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com