
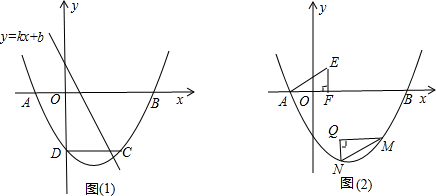
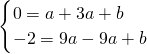 .
.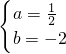 ,
, x2-
x2- x-2,
x-2, x2-
x2- x-2;
x-2; x2-
x2- x-2=0,
x-2=0, ,
, ,-2),
,-2), ,-1),
,-1), ,
, .
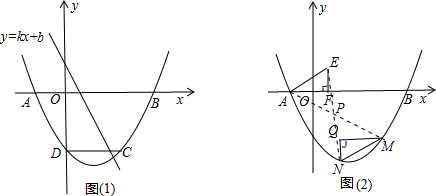
.
 x2-
x2- x-2中,得
x-2中,得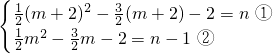 ,
, ,∴Q(1,-2),N(1,-3),
,∴Q(1,-2),N(1,-3), ,-2),过E作EF⊥AB于F,取EF的中点G,则G的坐标是(
,-2),过E作EF⊥AB于F,取EF的中点G,则G的坐标是( ,-1),则过G的直线(直线与AB和CD相交)都能把等腰梯形ABCD的面积二等份,把G的坐标代入y=kx+1即可求出答案;
,-1),则过G的直线(直线与AB和CD相交)都能把等腰梯形ABCD的面积二等份,把G的坐标代入y=kx+1即可求出答案; x2-
x2- x-2求出N的坐标,根据对称求出QF,即可求出P的坐标.
x-2求出N的坐标,根据对称求出QF,即可求出P的坐标.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
 积为常数时,矩形ABCD需要满足什么条件并说明理由.
积为常数时,矩形ABCD需要满足什么条件并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 ,且OA⊥AB,∠COB=45°.
,且OA⊥AB,∠COB=45°.| PM |
| OA |
| PN |
| BC |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com