
| A. | 一组数据-2,-1,0,1,1,2的中位数是0 | |
| B. | 质检部门要了解一批灯泡的使用寿命,应当采用普查的调查方式 | |
| C. | 购买一张福利彩票中奖是一个确定事件 | |
| D. | 分别写有三个数字-1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为$\frac{1}{3}$ |
分析 根据中位数、全面调查和抽样调查、事件的分类以及概率的求法分别对每一项进行分析,即可得出答案.
解答 解:A、数据-2,-1,0,1,1,2的中位数是$\frac{0+1}{2}$=$\frac{1}{2}$,故本选项错误;
B、质检部门要了解一批灯泡的使用寿命,应当采用抽样调查方式,故本选项错误;
C、购买一张福利彩票中奖是一个不确定事件,故本选项错误;
D、分别写有三个数字-1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为$\frac{1}{3}$,故本选项正确;
故选D.
点评 此题考查了中位数、全面调查和抽样调查、事件的分类以及概率的求法.用到的知识点为:可能发生,也可能不发生的事件叫做随机事件;概率=所求情况数与总情况数之比.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
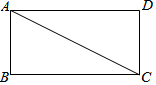 如图,已知在矩形ABCD中,AB=4,AD=8,将△ABC沿对角线AC翻折,点B落在点E处,联结DE,则DE的长为$\frac{12}{5}$$\sqrt{5}$.
如图,已知在矩形ABCD中,AB=4,AD=8,将△ABC沿对角线AC翻折,点B落在点E处,联结DE,则DE的长为$\frac{12}{5}$$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
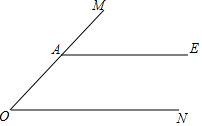 如图,A是∠MON边OM上一点,AE∥ON.
如图,A是∠MON边OM上一点,AE∥ON.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
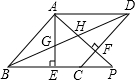 如图,在?ABCD中,过点A作AE⊥BC、AF⊥DC,垂足分别为点E、F,AE、AF分别交BD于点G、H,且AG=AH.
如图,在?ABCD中,过点A作AE⊥BC、AF⊥DC,垂足分别为点E、F,AE、AF分别交BD于点G、H,且AG=AH.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=4或m=4$\sqrt{3}$ | B. | 4≤m≤4$\sqrt{3}$ | C. | 2$\sqrt{3}$≤m≤4$\sqrt{3}$ | D. | 2$\sqrt{3}$≤m≤4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com