
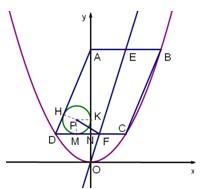
 上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为
上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为 。
。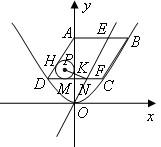
| 解:(1)∵点A的坐标为(0,16),且AB∥x轴 ∴B点纵坐标为4,且B点在抛物线 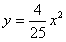 上 上 ∴点B的坐标为(10,16) 又∵点D、C在抛物线 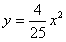 上,且CD∥x轴 上,且CD∥x轴 ∴D、C两点关于y轴对称 ∴DN=CN=5 ∴D点的坐标为(-5,4)。 (2)设E点的坐标为(a,16),则直线OE的解析式为: 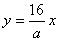 ∴F点的坐标为( 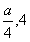 ) )由AE=a,DF=  且 且 得 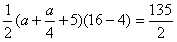 解得a=5。 |
|
| (3)连结PH,PM,PK ∵⊙P是△AND的内切圆,H,M,K为切点 ∴PH⊥AD,PM⊥DN,PK⊥AN 在Rt△AND中,由DN=5,AN=12,得AD=13 设⊙P的半径为r,则  r=2 在正方形PMNK中,PM=MN=2 ∴ 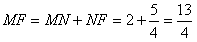 在Rt△PMF中,tan∠PMF=  。 。 |
 |


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
 CD的边长a等于点P,Q间的距离.
CD的边长a等于点P,Q间的距离.| CG | CB |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.
如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.查看答案和解析>>
科目:初中数学 来源: 题型:
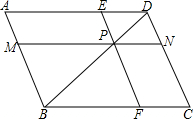 交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF.
交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF.| BP |
| PD |
| S平行四边形PEAM |
| S△ABD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 23、如图,已知平行四边形ABCD.
23、如图,已知平行四边形ABCD.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.
如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com