
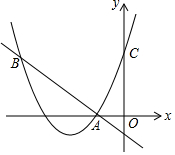
 如图,抛物线y=(x+2)2+m与y轴交于点C,与x轴交于点A(-1,0),点B在抛物线上,且与点C关于抛物线的对称轴对称,已知直线AB解析式为y=kx+b,求m的值及点B的横坐标,并直接写出满足(x+2)2+m<kx+b的x的取值范围.
如图,抛物线y=(x+2)2+m与y轴交于点C,与x轴交于点A(-1,0),点B在抛物线上,且与点C关于抛物线的对称轴对称,已知直线AB解析式为y=kx+b,求m的值及点B的横坐标,并直接写出满足(x+2)2+m<kx+b的x的取值范围. 分析 (1)先利用待定系数法先求出m,再求出点B坐标,利用方程组求出一次函数解析式.
(2)根据二次函数的图象在一次函数的图象上面即可写出自变量x的取值范围.
解答 解:(1)∵抛物线y=(x+2)2+m经过点A(-1,0),
∴0=1+m,
∴m=-1,
∴抛物线解析式为y=(x+2)2-1=x2+4x+3,
∴点C坐标(0,3),
∵对称轴x=-2,B、C关于对称轴对称,
∴点B坐标(-4,3);
(2)∵y=kx+b经过点A、B,
∴$\left\{\begin{array}{l}{-4k+b=3}\\{-k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
∴一次函数解析式为y=-x-1,
由图象可知,满足(x+2)2+m<kx+b的x的取值范围为-4<x<-1.
点评 本题考查二次函数与不等式、待定系数法等知识,解题的关键是灵活运用待定系数法确定好像解析式,学会利用图象根据条件确定自变量取值范围,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
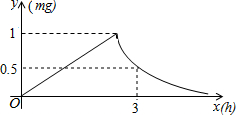 为了预防流感,某校在休息日用药熏消毒法对教室进行消毒,消毒过程中,室内每立方米空气中的含药量y(mg)与消毒开始后的时间x(h)之间的函数图象如图所示,其中药物释放完毕前y与x成正比例;药物释放完毕后,y与x成反比例.
为了预防流感,某校在休息日用药熏消毒法对教室进行消毒,消毒过程中,室内每立方米空气中的含药量y(mg)与消毒开始后的时间x(h)之间的函数图象如图所示,其中药物释放完毕前y与x成正比例;药物释放完毕后,y与x成反比例.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
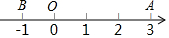 如图,已知数轴上的原点为O,点A表示3,点B表示-1,回答下列问题:
如图,已知数轴上的原点为O,点A表示3,点B表示-1,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com