
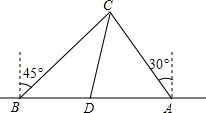
 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60($\sqrt{6}+\sqrt{2}$)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120($\sqrt{6}-\sqrt{2}$)海里.
为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60($\sqrt{6}+\sqrt{2}$)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120($\sqrt{6}-\sqrt{2}$)海里.分析 (1)如图所示,过点C作CE⊥AB于点E,可求得∠CBD=45°,∠CAD=60°,设CE=x,在Rt△CBE与Rt△CAE中,分别表示出BE、AE的长度,然后根据AB=60($\sqrt{6}+\sqrt{2}$)海里,代入BE、AE的式子,求出x的值,继而可求出AC、BC的长度;
(2)如图所示,过点D作DF⊥AC于点F,在△ADF中,根据AD的值,利用三角函数的知识求出DF的长度,然后与100比较,进行判断.
解答 解: (1)如图所示,过点C作CE⊥AB于点E,
(1)如图所示,过点C作CE⊥AB于点E,
可得∠CBD=45°,∠CAD=60°,
设CE=x,
在Rt△CBE中,BE=CE=x,
在Rt△CAE中,AE=$\frac{\sqrt{3}}{3}$x,
∵AB=60($\sqrt{6}+\sqrt{2}$)海里,
∴x+$\frac{\sqrt{3}}{3}$x=60($\sqrt{6}+\sqrt{2}$),
解得:x=60$\sqrt{6}$,
则AC=$\frac{2\sqrt{3}}{3}$x=120$\sqrt{2}$,
BC=$\sqrt{2}$x=120$\sqrt{3}$,
答:A与C的距离为120$\sqrt{2}$海里,B与C的距离为120$\sqrt{3}$海里;
(2)如图所示,过点D作DF⊥AC于点F,
在△ADF中,
∵AD=120($\sqrt{6}-\sqrt{2}$),∠CAD=60°,
∴DF=ADsin60°=180$\sqrt{2}$-60$\sqrt{6}$≈106.8>100,
故海监船沿AC前往C处盘查,无触礁的危险.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据题目中所给方向角构造直角三角形,然后利用三角函数的知识求解,难度适中.


科目:初中数学 来源: 题型:解答题
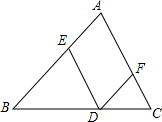 已知D为△ABC边BC上的一个动点(不与B,C重合),过D作DE∥AC交AB于点E,作DF∥AB交AC于点F.
已知D为△ABC边BC上的一个动点(不与B,C重合),过D作DE∥AC交AB于点E,作DF∥AB交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
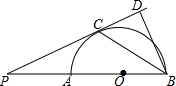 如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售价x(元/件) | … | 110 | 115 | 120 | 125 | 130 | … |
| 销售量y(件) | … | 50 | 45 | 40 | 35 | 30 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com