
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).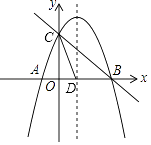
(1)求抛物线的解析式
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,请直接写出P点的坐标;如果不存在,请说明理由.
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?请求出△CBF的最大面积及此时E点的坐标.
【答案】
(1)
解:∵A(﹣1,0),C(0,2)在抛物线y= ![]() x2+bx+c上,
x2+bx+c上,
∴ 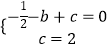 ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+2;
x+2;
(2)
解:∵y=﹣ ![]() x2+
x2+ ![]() x+2=﹣
x+2=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴抛物线对称轴为直线x= ![]() ,
,
∴D( ![]() ,0),且C(0,2),
,0),且C(0,2),
∴CD= ![]() =
= ![]() ,
,
∵点P在对称轴上,
∴可设P( ![]() ,t),
,t),
∴PD=|t|,PC= ![]() ,
,
当PD=CD时,则有|t|= ![]() ,解得t=±
,解得t=± ![]() ,此时P点坐标为(
,此时P点坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() );
);
当PC=CD时,则有 ![]() =
= ![]() ,解得t=0(与D重合,舍去)或t=4,此时P点坐标为(
,解得t=0(与D重合,舍去)或t=4,此时P点坐标为( ![]() ,4);
,4);
综上可知存在满足条件的点P,其坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,4);
,4);
(3)
解:当y=0时,即﹣ ![]() x2+
x2+ ![]() x+2=0,解得x=﹣1或x=4,
x+2=0,解得x=﹣1或x=4,
∴A(﹣1,0),B(4,0),
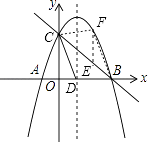
设直线BC解析式为y=kx+s,由题意可得 ![]() ,解得
,解得 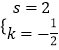 ,
,
∴直线BC解析式为y=﹣ ![]() x+2,
x+2,
∵点E是线段BC上的一个动点,
∴可设E(m,﹣ ![]() m+2),则F(m,﹣
m+2),则F(m,﹣ ![]() m2+
m2+ ![]() m+2),
m+2),
∴EF=﹣ ![]() m2+
m2+ ![]() m+2﹣(﹣
m+2﹣(﹣ ![]() m+2)=﹣
m+2)=﹣ ![]() m2+2m=﹣
m2+2m=﹣ ![]() (m﹣2)2+2,
(m﹣2)2+2,
∴S△CBF= ![]() ×4EF=2[=﹣
×4EF=2[=﹣ ![]() (m﹣2)2+2]=﹣(m﹣2)2+4,
(m﹣2)2+2]=﹣(m﹣2)2+4,
∵﹣1<0,
∴当m=2时,S△CBF有最大值,最大值为4,
此时﹣ ![]() x+2=1,
x+2=1,
∴E(2,1),即E为BC的中点,
∴当E运动到BC的中点时,△CBF的面积最大,最大面积为4,此时E点坐标为(2,1).
【解析】(1)由A、C的坐标,利用待定系数法可求得抛物线的解析式;(2)可设出P点坐标,则可表示出PC、PD和CD的长,分PD=CD、PC=CD两种情况分别得到关于P点坐标的方程,可求得P点坐标;(3)由B、C的坐标可求得直线BC的解析式,可设出E点坐标,则可表示出F点的坐标,从而可表示出EF的长,可表示出△CBF的面积,再利用二次函数的性质可求得其最大值及此时点E的坐标.


科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD对折后再展开,得到折痕EF,M是BC上一点,沿着AM再次折叠纸片,使得点B恰好落在折痕EF上的点B′处,连接AB′、BB′.
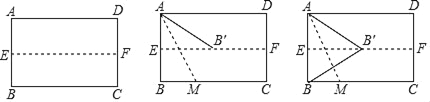
判断△AB′B的形状为 ;
若P为线段EF上一动点,当PB+PM最小时,请描述点P的位置为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图: 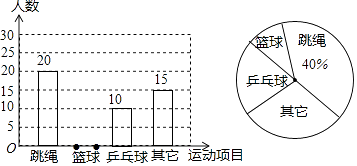
(1)在这次调查中,喜欢篮球项目的同学有人,在扇形统计图中,“乒乓球”的百分比为%,如果学校有800名学生,估计全校学生中有人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1,系数和为2;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1,系数和为4;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1,系数和为8……

根据以上规律,解答下列问题:
(1)(a+b)4的展开式共有多少项,系数分别为多少;
(2)写出(a+b)5的展开式;
(3)(a+b)n的展开式共有多少项,系数和为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2,正确的个数为( ) 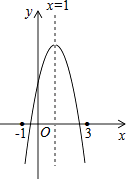
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备购进两种摩托车共25辆,预计投资10万元,现有甲、乙、丙三种摩托车供选购,甲种每辆4200元,可获利400元;乙种每辆3700元,可获利350元;丙种每辆3200元,可获利200元.要求10万元资金全部用完.
(1)请你帮助该商场设计进货方案;
(2)从销售利润上考虑,应选择哪种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com