
分析 首先分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{4x-10<2①}\\{\frac{3x-1}{2}≥1②}\end{array}\right.$,
由不等式①得:x<3;
由不等式②得:x≥1,
所以原不等式组的解集为:1≤x<3,
在数轴上表示: .
.
点评 此题主要考查了解一元一次不等式组,以及在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.


科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的网格中.
如图,在边长为1个单位长度的小正方形组成的网格中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
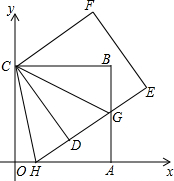 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连结CH、CG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连结CH、CG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
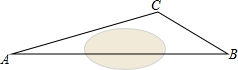 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.
如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
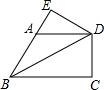 如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )
如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )| A. | 6+$\sqrt{3}$ | B. | 6+2$\sqrt{3}$ | C. | 7+$\sqrt{3}$ | D. | 7+2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在菱形ABCD中,E、F分别为边AD、CD上的点,且AE=CF,BE和BF交AC于点M、N.
如图,在菱形ABCD中,E、F分别为边AD、CD上的点,且AE=CF,BE和BF交AC于点M、N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com