
如图,某中学校园有一块长为35m,宽为16m的长方形空地,其中有一面已经铺设长为26m的篱笆围墙,学校设计在这片空地上,利用这面围墙和用尽已有的可制作50m长的篱笆材料,围成一个矩形花园或围成一个半圆花园,请回答以下问题:

(1)能否围成面积为300m2的矩形花园?若能,请写出其中一种设计方案,若不能,请说明理由.
(2)若围成一个半圆花园,则该如何设计?请写出你的设计方案.(π取3.14)
(3)围成的各种设计中,最大面积是多少?
(1)能,设计方案见解析;(2)设计方案见解析;(3)343.43m2.
【解析】
试题分析:(1)首先表示出矩形的长与宽,利用矩形面积得出等式,进而解方程得出;
(2)利用已知得出设新增加am,则半圆弧长为: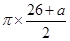 ,进而得出a的值,即可得出答案;
,进而得出a的值,即可得出答案;
(3)利用二次函数最值求法得出矩形最值再利用半圆面积公式得出半圆面积,进而比较即可.
试题解析:(1)设垂直于已经铺设长为26m的篱笆围墙的一边为xm,则平行于原篱笆的长为(50-2x)m,
根据题意得出:x(50-2x)=300,
解得:x1=10,x2=15,
当x=10,则50-20=30>26,故不合题意舍去,
∴能围成面积为300m2的矩形花园,此时长为20m,宽为15m;
(2)∵当r=13时,∴l半圆=πr=3.14×13=40.82<50,
∴半圆的直径应大于26m,设新增加am,则半圆弧长为: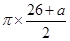 ,
,
∴a+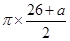 =50,
=50,
解得:a≈3.57,
∴半圆直径为:26+3.57=29.57(m),
∴半圆的半径为:14.79m;
(3)S1=x(50-2x)=-2x2+50x,
当x=12.5时,S最大= =312.5(m2),
=312.5(m2),
S半圆=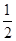 π×14.792≈343.43(m2),
π×14.792≈343.43(m2),
∴围成的各种设计中,最大面积是半圆面积为343.43m2.
考点: 1.二次函数的应用;2.一元二次方程的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
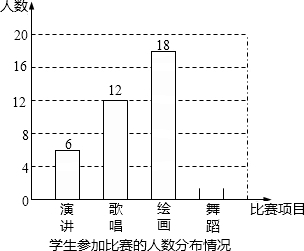 赛的人数之比为1:3.请你根据以上信息回答下列问题:
赛的人数之比为1:3.请你根据以上信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某中学校园有一块长为35m,宽为16m的长方形空地,其中有一面已经铺设长为26m的篱笆围墙,学校设计在这片空地上,利用这面围墙和用尽已有的可制作50m长的篱笆材料,围成一个矩形花园或围成一个半圆花园,请回答以下问题:
如图,某中学校园有一块长为35m,宽为16m的长方形空地,其中有一面已经铺设长为26m的篱笆围墙,学校设计在这片空地上,利用这面围墙和用尽已有的可制作50m长的篱笆材料,围成一个矩形花园或围成一个半圆花园,请回答以下问题:查看答案和解析>>
科目:初中数学 来源:活学巧练九年级数学上 题型:044
如图,某中学有一块长为a m、宽为b m的矩形场地,计划在该场地上修筑宽都为2m的两条互相垂直的道路,余下的4块矩形小场地建成草坪.
(1)请分别写出每条道路的面积(用含a或含b的代数式表示).
(2)已知a∶b=2∶1,并且4块草坪的面积之和为312m2,试求原来矩形场地的长与宽各为多少?
(3)在(2)的条件下,为进一步美化校园,根据实际情况,学校决定对整个矩形场地作如下设计(要求同时符合下述两个条件):
条件①:在每块草坪上各修建一个面积尽可能大的菱形花圃(花圃各边必须分别与所在草坪的对角线平行),并且其中有两个花圃的面积之差为13m2;
条件②:整个矩形场地(包括道路、草坪、花圃)为轴对称图形.
请你画出符合上述设计方案的一种草图(不必说明画法与根据),并求出每个菱形花圃的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某中学校园有一块长为35m,宽为16m的长方形空地,其中有一面已经铺设长为26m的篱笆围墙,学校设计在这片空地上,利用这面围墙和用尽已有的可制作50m长的篱笆材料,围成一个矩形花园或围成一个半圆花园,请回答以下问题:
如图,某中学校园有一块长为35m,宽为16m的长方形空地,其中有一面已经铺设长为26m的篱笆围墙,学校设计在这片空地上,利用这面围墙和用尽已有的可制作50m长的篱笆材料,围成一个矩形花园或围成一个半圆花园,请回答以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com