
 已知,如图,正方形ABCD的边长为12,菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,AH=4,连接CF.
已知,如图,正方形ABCD的边长为12,菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,AH=4,连接CF.分析 (1)由于四边形ABCD为正方形,四边形HEFG为菱形,那么∠D=∠A=90°,HG=HE,而AH=DG=2,易证△AHE≌△DGH,从而有∠DHG=∠HEA,等量代换可得∠AHE+∠DHG=90°,易证四边形HEFG为正方形;再证明△AHE≌△MFG即可解决问题;
(2)欲求△FCG的面积,由已知得CG的长易求,只需求出GC边的高即可;
(3)不能.如果24-2x=4,x=10,此时DG=10,GH=HE=$\sqrt{1{0}^{2}+{8}^{2}}$=$\sqrt{164}$,易知AE=$\sqrt{E{H}^{2}-A{H}^{2}}$=$\sqrt{164-16}$=$\sqrt{148}$>12,推出点E不在正方形的边AB上,不合题意;
解答 解:(1)在△HDG和△AEH中,
∵四边形ABCD是正方形,∴∠D=∠A=90°,
∵四边形EFGH是菱形,
∴HG=HE,
∵DG=AH=4,
在Rt△HDG和Rt△AEH中,
$\left\{\begin{array}{l}{HG=HE}\\{DG=AH}\end{array}\right.$,
∴Rt△HDG≌Rt△AEH,
∴∠DHG=∠AEH,AE=HD=8,
∴∠DHG+∠AHE=90°
∴∠GHE=90°,
过F作FM⊥CD,垂足为M,连接GE
∵CD∥AB,
∴∠AEG=∠MGE,
∵GF∥HE,
∴∠HEG=∠FGE,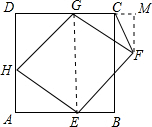
∴∠AEH=∠FGM,
在Rt△AHE和Rt△GFM中,
$\left\{\begin{array}{l}{∠A=∠M=90°}\\{∠AEH=∠FGM}\\{HE=FG}\end{array}\right.$,
∴Rt△AHE≌Rt△MFG,
∴MF=AH=4,GM=AE=8,
∴S△FCG=$\frac{1}{2}$•CG•FM=$\frac{1}{2}$×8×4=16.
(2)由(1)可知,Rt△AHE≌Rt△MFG,
∴FM=AH=4,
∵GC=12-x,
∴S△CFG=$\frac{1}{2}$•CG•FM=24-2x
(3)不能.
理由:如果24-2x=4,x=10,
此时DG=10,GH=HE=$\sqrt{1{0}^{2}+{8}^{2}}$=$\sqrt{164}$,
易知AE=$\sqrt{E{H}^{2}-A{H}^{2}}$=$\sqrt{164-16}$=$\sqrt{148}$>12,
∴点E不在正方形的边AB上,不合题意,
∴△GCF的面积不可能为4.
点评 本题考查了正方形的性质、菱形的性质、全等三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
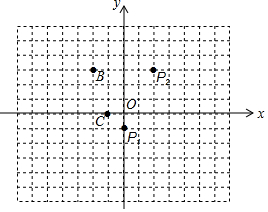 阅读理解:我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).
阅读理解:我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知函数y1=x2-2x-3.
已知函数y1=x2-2x-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
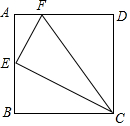 如图,已知正方形ABCD的边长为4,E为AB中点,F为AD上的一点,且AF=$\frac{1}{4}$AD,请你判断△EFC的形状并说明理由.
如图,已知正方形ABCD的边长为4,E为AB中点,F为AD上的一点,且AF=$\frac{1}{4}$AD,请你判断△EFC的形状并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,AD是BC边上的中线,O是AB的中点,延长DO至E,使OE=OD,连接AE、BE.
如图,在△ABC中,AB=AC,AD是BC边上的中线,O是AB的中点,延长DO至E,使OE=OD,连接AE、BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com