
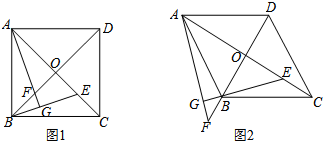
分析 (1)根据正方形的对角线相等且互相垂直平分可得OA=OB,再根据同角的余角相等求出∠AFO=∠BEO,然后利用“角角边”证明△AOF和△BOE全等,根据全等三角形对应边相等证明即可;
(2)根据菱形的对角线互相垂直可得AC⊥BD,对角线平分一组对角可得∠ABO=60°,再根据等角的余角相等求出∠AFO=∠BEO,然后证明△AOF和△BOE相似,根据相似三角形对应边成比例可得 $\frac{OF}{OE}$=$\frac{AO}{OB}$,再根据锐角三角形函数的定义解答;
解答 证明:(1)∵四边形ABCD是正方形,对角线的交点为O,
∴AC=BD,OA=OC,OB=OD,
∴OA=OB,
∵AC⊥BD,AG⊥BE,
∴∠FAO+∠AFO=90°,∠EAG+∠AEG=90°,
∴∠AFO=∠BEO,
在△AOF和△BOE中,
$\left\{\begin{array}{l}{∠AFO=∠BEO}\\{∠FOA=∠EOB}\\{OA=OB}\end{array}\right.$,
∴△AOF≌△BOE(AAS),
∴OE=OF;
(2)OF=$\sqrt{3}$OE.
理由:∵四边形ABCD是菱形,对角线的交点为O,∠ABC=120°
∴AC⊥BD,∠ABO=60°,
∴∠FAO+∠AFO=90°,
∵AG⊥BE,
∴∠EAG+∠BEA=90°.
∴∠AFO=∠BEO,
又∵∠AOF=∠BOE=90°,
∴△AOF∽△BOE,
∴$\frac{OF}{OE}$=$\frac{AO}{OB}$,
∵∠ABO=60°,AC⊥BD,
∴$\frac{AO}{OB}$=tan60°=$\sqrt{3}$.
∴OF=$\sqrt{3}$OE;
点评 本题是四边形综合题型,主要利用了正方形的性质,全等三角形的判定与性质,菱形的对角线互相垂直平分的性质,等腰梯形的性质,以及相似三角形的判定与性质,锐角三角形函数,综合性较强,解题的关键是正确寻找全等三角形或相似三角形解决问题,属于中考常考题型.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
| 路程(千米) | 运费(元/吨•千米) | |||
| 甲库 | 乙库 | 甲库 | 乙库 | |
| A地 | 20 | 15 | 12 | 12 |
| B地 | 25 | 20 | 10 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
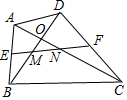 如图.在四边形ABCD中.AC=BD,E,F分别为AB,CD的中点(O,M,N不重合),仔细观察你会发观.无论四边形ABCD的形状如何变化,只要保待对角线相等,则EF与两条对角线围成的三角形总是等腰三角形(图中的△OMN),请说明理由.
如图.在四边形ABCD中.AC=BD,E,F分别为AB,CD的中点(O,M,N不重合),仔细观察你会发观.无论四边形ABCD的形状如何变化,只要保待对角线相等,则EF与两条对角线围成的三角形总是等腰三角形(图中的△OMN),请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com