
 (2013•门头沟区一模)为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度CD=3m,标杆与旗杆的水平距离BD=15 m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,E、C、A三点共线,则旗杆AB的高度为
(2013•门头沟区一模)为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度CD=3m,标杆与旗杆的水平距离BD=15 m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,E、C、A三点共线,则旗杆AB的高度为| CG |
| AH |
| EG |
| EH |
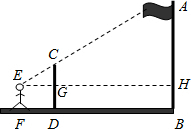 解:∵CD⊥FB,AB⊥FB,
解:∵CD⊥FB,AB⊥FB,| CG |
| AH |
| EG |
| EH |
| CD-EF |
| AH |
| FD |
| FD+BD |
| 3-1.6 |
| AH |
| 2 |
| 2+15 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
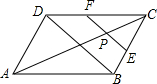 (2013•门头沟区二模)如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E、F.设CP=x,EF=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
(2013•门头沟区二模)如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E、F.设CP=x,EF=y,则下列图象中,能表示y与x的函数关系的图象大致是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•门头沟区二模)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB的高度是
(2013•门头沟区二模)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB的高度是| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
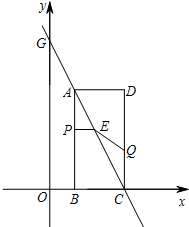 (2013•门头沟区二模)如图,在平面直角坐标系xOy中,已知矩形ABCD的两个顶点B、C的坐标分别是B(1,0)、C(3,0).直线AC与y轴交于点G(0,6).动点P从点A出发,沿线段AB向点B运动.同时动点 Q从点C出发,沿线段CD向点D运动.点P、Q的运动速度均为每秒1个单位,运动时间为t秒.过点P作PE⊥AB交AC于点E.
(2013•门头沟区二模)如图,在平面直角坐标系xOy中,已知矩形ABCD的两个顶点B、C的坐标分别是B(1,0)、C(3,0).直线AC与y轴交于点G(0,6).动点P从点A出发,沿线段AB向点B运动.同时动点 Q从点C出发,沿线段CD向点D运动.点P、Q的运动速度均为每秒1个单位,运动时间为t秒.过点P作PE⊥AB交AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com