
将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.
(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断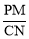 的值是否随着α的变化而变化?如果不变,请求出
的值是否随着α的变化而变化?如果不变,请求出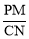 的值;反之,请说明理由.
的值;反之,请说明理由.

(1)120°;(2)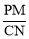 的值不随着α的变化而变化,是定值
的值不随着α的变化而变化,是定值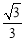 .
.
【解析】
试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得CD=AD=BD=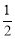 AB,根据等边对等角求出∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC﹣∠EDF计算即可得解.
AB,根据等边对等角求出∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC﹣∠EDF计算即可得解.
(2)根据同角的余角相等求出∠PDM=∠CDN,再根据然后求出△BCD是等边三角形,根据等边三角形的性质求出∠BCD=60°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CPD=60°,从而得到∠CPD=∠BCD,再根据两组角对应相等,两三角形相似判断出△DPM和△DCN相似,再根据相似三角形对应边成比例可得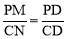 为定值.
为定值.
试题解析:【解析】
(1)∵∠ACB=90°,∠B=60°,∴∠A=30°.
∵点D为AB的中点,∴CD=AD=BD=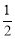 AB.∴∠ACD=∠A=30°.
AB.∴∠ACD=∠A=30°.
∴∠ADC=180°﹣30°×2=120°.
∴∠ADE=∠ADC﹣∠EDF=120°﹣90°=30°.
(2)∵∠EDF=90°,∴∠PDM+∠E′DF=∠CDN+∠E′DF=90°.∴∠PDM=∠CDN.
∵∠B=60°,BD=CD,∴△BCD是等边三角形.∴∠BCD=60°.
∵∠CPD=∠A+∠ADE=30°+30°=60°,∴∠CPD=∠BCD.
在△DPM和△DCN中,∵∠PDM=∠CDN,∠CPD=∠BCD,
∴△DPM∽△DCN.∴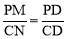 .
.
∵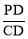 =tan∠ACD=tan30°=
=tan∠ACD=tan30°=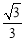 ,∴
,∴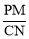 的值不随着α的变化而变化,是定值
的值不随着α的变化而变化,是定值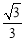 .
.
考点:1.面动旋转问题;2.旋转的性质;3.直角三角形斜边上中线的性质;4.等腰(边)三角形的判定和性质;5.三角形外角性质;6.相似三角形的判定和性质;7.锐角三角函数定义;8.特殊角的三角函数值.


科目:初中数学 来源:2014年初中毕业升学考试(湖南邵阳卷)数学(解析版) 题型:选择题
已知点M(1,a)和点N(2,b)是一次函数y=﹣2x+1图象上的两点,则a与b的大小关系是( )
A.a>b B.a=b C.a<b D.以上都不对
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南湘潭卷)数学(解析版) 题型:解答题
从全校1200名学生中随机选取一部分学生进行调查,调查情况:A、上网时间≤1小时;B、1小时<上网时间≤4小时;C、4小时<上网时间≤7小时;D、上网时间>7小时.统计结果制成了如图统计图:
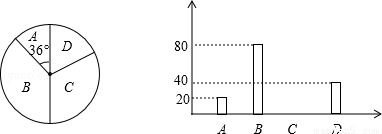
(1)参加调查的学生有 人;
(2)请将条形统计图补全;
(3)请估计全校上网不超过7小时的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com