
【题目】如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.
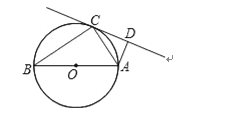
(1)求证:CD是⊙O的切线;
(2)若AD=1,OA=2,求AC的值.
【答案】(1)证明见解析;(2)2.
【解析】试题分析:(1)连接OC,由圆周角定理得出∠ACB=90°,由等腰三角形的性质得出∠B=∠BCO,证出∠OCD=∠OCA+∠BCO=∠ACB=90°,即可得出结论;
(2)证明△ACB∽△ADC,得出AC2=ADAB,即可得出结果.
试题解析:(1)证明:连接OC,如图所示:
∵AB是⊙O直径,
∴∠ACB=90°,
∵OB=OC,
∴∠B=∠BCO,
又∵∠ACD=∠B,
∴∠OCD=∠OCA+∠ACD=∠OCA+∠BCO=∠ACB=90°,
即OC⊥CD,
∴CD是⊙O的切线;
(2)解:∵AD⊥CD,
∴∠ADC=∠ACB=90°,
又∵∠ACD=∠B,
∴△ACB∽△ADC,
∴AC2=ADAB=1×4=4,
∴AC=2.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,若反比例函数y=﹣![]() 与一次函数y=mx﹣2的图象都经过点A(a,2)
与一次函数y=mx﹣2的图象都经过点A(a,2)
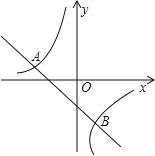
(1)求A点的坐标及一次函数的解析式;
(2)设一次函数与反比例函数图象的另一交点为B,求B点坐标,并利用函数图象写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
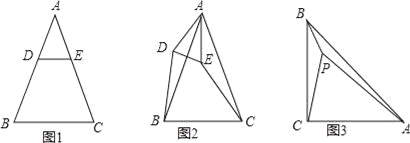
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 上升和下降是具有相反意义的量
B. 前进20米是具有相反意义的量
C. 向南走50米与向北走40米是具有相反意义的量
D. 收入20元与下降20米是具有相反意义的量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD四条边长分别为54 cm,48 cm,45 cm,63 cm,另一个和它相似的四边形最短边长为15 cm,则这个四边形最长边为( )
A. 16 cm B. 17 cm C. 18 cm D. 21 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( )
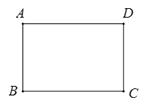
A. 6 B. 3 C. 2.5 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com