
如图,点C是l上任意一点,CA⊥CB且AC=BC,过点A作AM⊥l于点M,过点B作BN⊥l于N,则线段MN与AM、BN有什么数量关系,证明你的结论:
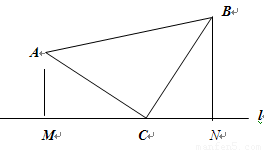
MN=AM+BN,证明见解析
【解析】MN=AM+BN …………1分
证明:∵CA⊥CB
∴∠ACM +∠BCN = 900
又∵BN⊥l于N,
∴ ∠CBN + ∠BCN = 900
∴ ∠ACM=∠CBN ………………………3分
又∵∠AMC =∠BNC=900,AC=BC,
∴ △AMC≌△CNB ………………………6分
∴AM=CN,BN=CM, ………………………8分
∴MN=AM+BN ………………………9分
由AM⊥l于点M,B作BN⊥l于N,可得∠AMC=∠BNC=90°,又由CA⊥CB,根据同角的余角相等,可得∠ACM=∠CBN,然后由AC=BC,利用AAS,即可判定△AMC≌△CNB,继而证得MN=AM+BN.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
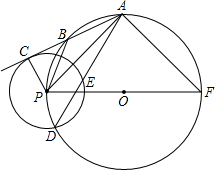 直径,设⊙O与⊙P的半径分别为R和r.
直径,设⊙O与⊙P的半径分别为R和r.查看答案和解析>>
科目:初中数学 来源: 题型:
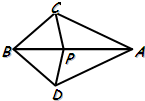 9、如图,点P是AB上任意一点,∠ABC=∠ABD,还应补充一个条件,才能推出△APC≌△APD.从下列条件中补充一个条件,不一定能推出△APC≌△APD的是( )
9、如图,点P是AB上任意一点,∠ABC=∠ABD,还应补充一个条件,才能推出△APC≌△APD.从下列条件中补充一个条件,不一定能推出△APC≌△APD的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
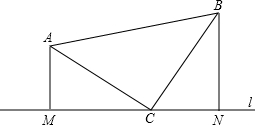 如图,点C是l上任意一点,CA⊥CB且AC=BC,过点A作AM⊥l于点M,过点B作BN⊥l于N,则线段MN与AM、BN有什么数量关系,证明你的结论:
如图,点C是l上任意一点,CA⊥CB且AC=BC,过点A作AM⊥l于点M,过点B作BN⊥l于N,则线段MN与AM、BN有什么数量关系,证明你的结论:查看答案和解析>>
科目:初中数学 来源:2012届河南信阳市二中中考模拟考试数学试卷(带解析) 题型:解答题
如图,点C是l上任意一点,CA⊥CB且AC=BC,过点A作AM⊥l于点M,过点B作BN⊥l于N,则线段MN与AM、BN有什么数量关系,证明你的结论: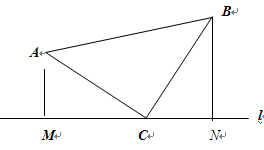
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com