
【题目】如图,△ABC中,∠C=90°,AD平分∠BAC,AD=4,CD=2,AC=2![]() ,则△ABD的面积是_______________.
,则△ABD的面积是_______________.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,河坝横断面背水坡AB的坡角是45°,背水坡AB长度为20 ![]() 米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】
米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】 
(1)求加固部分即△ABD的横截面的面积;
(2)若该堤坝的长度为100米,某工程队承包了这一加固的土石方工程,为抢在在汛期到来之际提前完成这一工程,现在每天完成的土方比原计划增加25%,这样实际比原计划提前10天完成了,求原计划每天完成的土方.【提示土石方=横截面x堤坝长度】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( ) ①AB∥CQ;②∠ACQ=60°;③AP2=AMAC;④若BP=PC,则PQ⊥AC.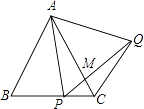
A.①②
B.①③
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
分数段(分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x≤90 | 16 | b% |
90≤x<100 | 4 | 10% |
请根据图表提供的信息,解答下列问题:
(1)表中的a= , b=;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是多少? 
查看答案和解析>>
科目:初中数学 来源: 题型:
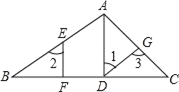
【题目】如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
(1)AD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD是△ABC的中线,∠ACE是△ABC的外角. 
(1)读下列语句,尺规作图,保留作图痕迹. ①作∠ACE的角平分线,交BA延长线于点F;
②过点D作DH∥AC,交AB于点H,连接CH.
(2)依据以上条件,解答下列问题. ①与△AHD面积相等的三角形是;
②若∠B=40°,∠F=30°,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教育网站对下载资源规定如下:若注册VIP用户,则下载每份资源收![]() 元,另外每年收500元的VIP会员费,若注册普通用户,则下载每份资源收
元,另外每年收500元的VIP会员费,若注册普通用户,则下载每份资源收![]() 元,不收其它费用
元,不收其它费用
![]() 分别写出注册VIP用户的收费
分别写出注册VIP用户的收费![]() 元
元![]() 和注册普通用户
和注册普通用户![]() 元
元![]() 与下载数量
与下载数量![]() 份
份![]() 之间的函数关系式
之间的函数关系式
![]() 某学校每年要下载1500份资源,那么注册哪种用户比较合算?
某学校每年要下载1500份资源,那么注册哪种用户比较合算?
![]() 一年内下载多少份资源是两种用户收费一样?
一年内下载多少份资源是两种用户收费一样?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com