已知:a,b,c是△ABC的三边长,c为整数,抛物线y=x2-(a+b)x+c2-8a-8与x轴相交于点M,N(点M在N的左侧),顶点为P,点(a-bsinC,m)与点(asinC-b,m)关于y轴对称.
(1)判断△ABC的形状;
(2)若抛物线与直线y=x-14相交于点P和D(6,-8),在抛物线上求作一点Q,使∠QMP=90°.
分析:(1)根据点(a-bsinC,m)与点(asinC-b,m)关于y轴对称,可得两点的横坐标互为相反数,由此可求得a、b的关系式,即可得出△ABC的形状.
(2)首先求出点P的坐标,再将P点坐标代入直线y=x-14中①,将D代入抛物线的解析式中②,联立①②所得式子,即可求出抛物线的解析式,进而可确定M、P的坐标;易求得直线MP的解析式,若∠QMP=90°,则直线MQ与直线MP的斜率的积为-1,不难求得直线MQ的解析式联立抛物线的解析式即可求出Q点的坐标.
解答:解:(1)∵点(a-bsinC,m)与点(asinC-b,m)关于y轴对称,
∴a-bsinC+asinC-b=(a-b)+(a-b)sinC=(a-b)(sinC+1)=0;
∵0°<∠C<180°,即sinC+1≠0,
∴a=b;即△ABC是等腰三角形.
(2)由(1)知:a=b,则y=x
2-2ax+c
2-8a-8,P(a,c
2-a
2-8a-8);
∵P点在直线y=x-14的图象上,
∴a-14=c
2-a
2-8a-8;①
∵抛物线过D(6,-8),
∴36-12a+c
2-8a-8=-8;②
联立①②,得:
| | a-14=c2-a2-8a-8 | | 36-12a+c2-8a-8=-8 |
| |
,
解得
(c取整数);
∴抛物线的解析式为y=x
2-10x+16,P(5,-9),M(2,0),N(8,0);
设直线MP的解析式为y=kx+b(k≠0),则:
,
解得
;
∴直线MP的解析式为y=-3x+6;
设直线MQ的解析式为y=mx+n(m≠0),由于∠PMQ=90°,
得mk=-1,即m=
;
则y=
x+n;已知M点坐标为(2,0),则有:
+n=0,n=-
;
∴直线MQ的解析式为y=
x-
;
联立抛物线的解析式,得:
,
解得
,
;
∴Q点的坐标为(
,
).
点评:此题是二次函数的综合题,涉及到三角函数、轴对称的性质、二次函数解析式的确定、函数图象交点坐标的求法等.难度较大.



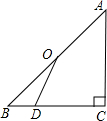 已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.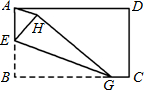 12、如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为
12、如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为