
��ͼ�����κ�����ͼ����x���ཻ�ڵ�A����3��0����B����1��0������y���ཻ�ڵ�C��0��3������P�Ǹ�ͼ���ϵĶ��㣻һ�κ���y=kx��4k��k��0����ͼ�����P��x���ڵ�Q��
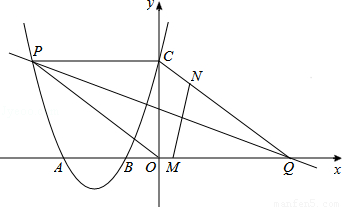
��1����ö��κ����Ľ���ʽ��
��2������P������Ϊ����4��m��ʱ����֤����OPC=��AQC��
��3����M��N�ֱ����߶�AQ��CQ�ϣ���M��ÿ��3����λ���ȵ��ٶȴӵ�A���Q�˶���ͬʱ����N��ÿ��1����λ���ȵ��ٶȴӵ�C���Q�˶�������M��N����һ�㵽��Q��ʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룮����AN������AMN��������ʱ��
����t��ֵ��
��ֱ��PQ�ܷ�ֱƽ���߶�MN�����ܣ��������ʱ��P�����ꣻ�����ܣ���˵��������ɣ�
�⣺��1���߶��κ�����ͼ����x���ཻ�ڵ�A����3��0����B����1��0����
������κ����Ľ���ʽΪ��y=a��x+3����x+1����
�߶��κ�����ͼ����C��0��3������3=a��3��1�����a=1��
����κ����Ľ���ʽΪ��y=��x+3����x+1������y =x2+4x+3��
��2��֤�����ڶ��κ�������ʽy=x2+4x+3�У���x=��4ʱ��y=3����P����4��3����
��P����4��3����C��0��3������PC=4��PC��x�ᡣ
��һ�κ���y=kx��4k��k��0����ͼ��x���ڵ�Q����y=0ʱ��x=4����Q��4��0����OQ=4��
��PC=OQ��
�֡�PC��x�ᣬ���ı���POQC��ƽ���ı��Ρ�
���OPC=��AQC��
��3������Rt��COQ�У�OC=3��OQ=4���ɹ��ɶ����ã�CQ=5��
���ͼ1��ʾ������N��ND��x���ڵ�D����ND��OC��

���QND�ס�QCO��
�� ����
���� ��
��
��ã� ��
��
��S=S��AMN����
 ��
��
�֡�AQ=7����M���ٶ���ÿ��3����λ���ȣ�
���M�����յ��ʱ��Ϊt= ��
��
�� ��0��t��
��0��t�� ����
����
�� ��0��
��0�� ��
�� ����x��
����x�� ʱ��y��x�����������
ʱ��y��x�����������
�൱t= ʱ����AMN��������
ʱ����AMN��������
�ڼ���ֱ��PQ�ܹ���ֱƽ���߶�MN������QM=QN����PQ��MN��PQƽ�֡�AQC��
��QM=QN���ã�7��3t=5��t�����t=1��
��ʱ��M���O�غϣ����ͼ2��ʾ��

��PQ��OC���ڵ�E���ɣ�2����֪���ı���POQC��ƽ���ı��Σ�
��OE=CE��
�ߵ�E��CQ�ľ���С��CE��
���E��CQ�ľ���С��OE��
��OE��x�ᣬ
��PQ���ǡ�AQC��ƽ���ߣ��������ì�ܡ�
��ֱ��PQ���ܴ�ֱƽ���߶�MN
��������
�����������1�����ý���ʽ��������ߵĽ���ʽ��
��2��֤���ı���POQC��ƽ���ı��Σ�����۵�֤��
��3���������AMN����ı���ʽ�����ö��κ��������ʣ������AMN������ʱt��ֵ��
������ֱ��PQ�ϵĵ㵽��AQC���ߵľ��벻��ȣ���ֱ��PQ����ƽ�֡�AQC������ֱ��PQ���ܴ�ֱƽ���߶�MN��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012�걱���л���Ů����ѧ���꼶��һѧ�����п�����ѧ�� ���ͣ������
��ͼ�Ƕ��κ��� ��ͼ���䶥������ΪM(1,-4).
��ͼ���䶥������ΪM(1,-4).
��С��1����1�����ͼ���� ��Ľ���A,B�����ꣻ
��Ľ���A,B�����ꣻ
��С��2����2���ڶ��κ�����ͼ�����Ƿ���ڵ�P��ʹ ,�����ڣ����P������ꣻ�������ڣ���˵�����ɣ�
,�����ڣ����P������ꣻ�������ڣ���˵�����ɣ�
��С��3����3�������κ�����ͼ���� ���·��IJ�����
���·��IJ����� �ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ������������µ�ͼ��ش𣺵�ֱ��
�ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ������������µ�ͼ��ش𣺵�ֱ�� ���ͼ��������������ʱ��
���ͼ��������������ʱ�� ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013���Ϻ����п���ѧģ���Ծ��������������棩 ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011���Ϻ����ֶ������п���ѧ��ģ�Ծ��������棩 ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com