
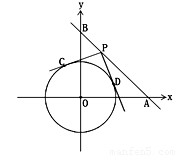
在平面直角坐标中,直线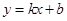 (
(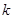 为常数且
为常数且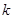 ≠0),分别交
≠0),分别交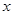 轴,
轴,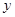 轴于点
轴于点 、
、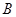 、⊙
、⊙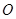 的半径为
的半径为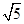 个单位长度,如图,若点
个单位长度,如图,若点 在
在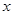 轴正半轴上,点
轴正半轴上,点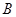 在
在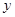 轴的正半轴上,且
轴的正半轴上,且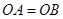 。
。
(1)求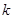 的值。
的值。
(2)若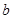 =4,点P为直线
=4,点P为直线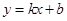 上的一个动点过点
上的一个动点过点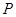 作⊙
作⊙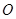 的切线
的切线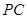 、
、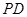 切点分别为
切点分别为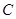 、
、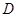 。当
。当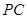 ⊥
⊥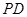 时,求点
时,求点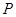 的坐标。
的坐标。
(1)k=-1;(2)(1,3)或(3,1)
【解析】
试题分析:(1)由题意可得B的坐标,又由OA=OB可得到点A的坐标,把坐标代入解析式消去b,可求得k的值;
(2)要求p点的坐标,可先设出坐标,找关系列出方程可求解,要列方程必须先求出OP的大小,于是借助等腰直角三角形进行解答,答案可得.
(1)根据题意得:B的坐标为(0,b),
∴OA=OB=b,
∴A的坐标为(b,0),
代入y=kx+b得k=-1.
(2)过P作x轴的垂线,垂足为F,连结OD.
∵PC、PD是⊙O的两条切线,∠CPD=90°,
∴∠OPD=∠OPC=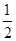 ∠CPD=45°,
∠CPD=45°,
∵∠PDO=90°,∠POD=∠OPD=45°
∴OD=PD=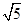 ,OP=
,OP=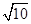 .
.
∵P在直线y=-x+4上,
设P(m,-m+4),P点在第一象限
则OF=m,PF=-m+4,
∵∠PFO=90°, OF2+PF2=PO2,
∴ m2+
(-m+4)2=(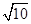 )2,
)2,
解得m=1或3,
∴P的坐标为(1,3)或(3,1).
考点:本题考查了一次函数的综合应用
点评:有函数参与的几何题往往要找出等量关系后利用函数的解析式列方程进行解答,这种数形结合的思想非常重要,要认真掌握.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
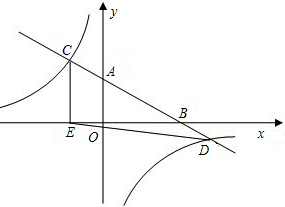 反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=
反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
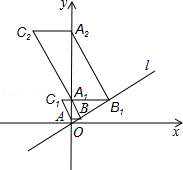
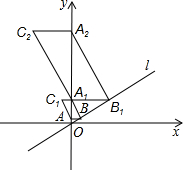 (2013•铁岭)如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1,以A1B.BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是
(2013•铁岭)如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1,以A1B.BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1,以A1B.BA为邻边作![]() ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作
ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作![]() A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .
A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1,以A1B.BA为邻边作![]() ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作
ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作![]() A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .
A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(辽宁铁岭卷)数学(解析版) 题型:填空题
如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1,以A1B.BA为邻边作 ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作
ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作 A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .
A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com