
某公司有 型产品40件,
型产品40件, 型产品60件,分配给下属甲、乙两
型产品60件,分配给下属甲、乙两 个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
|
|
| |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(1)设分配给甲店 型产品
型产品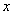 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为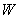 (元),求
(元),求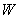 关于
关于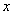 的函数关系式,并求出
的函数关系式,并求出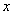 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配 方案,并将
方案,并将 各种方案设计出来;
各种方案设计出来;
(3)为了促销,公司决定仅对甲店 型产品让利销售,每件让利
型产品让利销售,每件让利 元,但让利后
元,但让利后 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店 型产品的每件利润.甲店的
型产品的每件利润.甲店的 型产品以及乙店的
型产品以及乙店的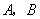 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
依题意,甲店 型产品有
型产品有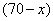 件,乙店
件,乙店 型有
型有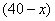 件,
件, 型有
型有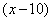 件,则
件,则
(1)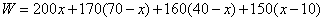
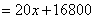 .
.
由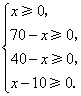 解得
解得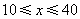 .····················· 3分
.····················· 3分
(2)由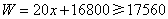 ,
,
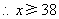 .
.
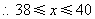 ,
,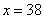 ,39,40.
,39,40.
 有三种不同的分配方案.
有三种不同的分配方案.
①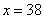 时,甲店
时,甲店 型38件,
型38件, 型32件,乙店
型32件,乙店 型2件,
型2件, 型28件.
型28件.
②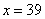 时,甲店
时,甲店 型39件,
型39件, 型31件,乙店
型31件,乙店 型1件,
型1件, 型29件.
型29件.
③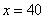 时,甲店
时,甲店 型40件,
型40件, 型30件,乙店
型30件,乙店 型0件,
型0件, 型30件.···· 3分
型30件.···· 3分
(3)依题意:

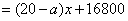 .
.
①当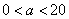 时,
时,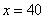 ,即甲店
,即甲店 型40件,
型40件, 型30件,乙店
型30件,乙店 型0件,
型0件, 型30件,能使总利润达到最大.
型30件,能使总利润达到最大.
②当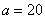 时,
时,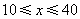 ,符合题意的各种方案,使总利润都一样.
,符合题意的各种方案,使总利润都一样.
③当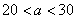 时,
时,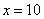 ,即甲店
,即甲店 型10件,
型10件, 型60件,乙店
型60件,乙店 型30件,
型30件, 型0件,能使总利润达到最大. 4分
型0件,能使总利润达到最大. 4分


科目:初中数学 来源: 题型:
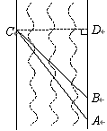
在一次数学活动课上,某校初三数学老师带领学生去测河宽,如图13所示,某学生在河东岸点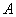 处观测到河对岸水边有一点
处观测到河对岸水边有一点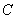 ,测得
,测得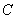 在
在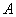 北偏西
北偏西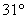 的方向上,沿河岸向北前行20米到达
的方向上,沿河岸向北前行20米到达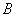 处,测得
处,测得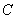 在
在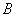 北偏西
北偏西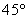 的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈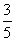 ,sin31°≈
,sin31°≈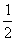 )
) 
查看答案和解析>>
科目:初中数学 来源: 题型:
在下列条件中:①∠A+∠B=∠C;②∠A:∠B∠:∠C=1:2:3;③∠A=90°-∠B;④∠A=∠B=∠C,能确定△ABC是直角三角形的条件有( )个.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
A.△ACE≌△BCD B.△BGC≌△AFC C.△DCG≌△ECF D.△ADB≌△CEA

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com