
 :
:
 b(不合题意,舍去),
b(不合题意,舍去), a,
a, a代入①得:c2=3a2,即c=
a代入①得:c2=3a2,即c= a,
a, :
: .
. :
:


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
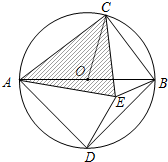 若在⊙O内存在点E,使AE=AD,CB=CE.
若在⊙O内存在点E,使AE=AD,CB=CE.查看答案和解析>>
科目:初中数学 来源:2011-2012学年广东省汕头市九年级一元二次方程单元卷.doc 题型:解答题
.(10分)已知关于x的方程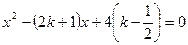 ,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。
,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。
24.(11分)现定义一种新运算:“※”,使得a※b=4ab
(1)求4※7的值
(2)求x※x+2※x-2※4=0中x的值。
(3)不论x是什么数,总有a※x=x,求a的值。
查看答案和解析>>
科目:初中数学 来源:2012届广东省汕头市九年级一元二次方程单元卷 题型:选择题
.(10分)已知关于x的方程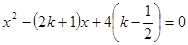 ,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。
,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。
24.(11分)现定义一种新运算:“※”,使得a※b=4ab
(1)求4※7的值
(2)求x※x+2※x-2※4=0中x的值。
(3)不论x是什么数,总有a※x=x,求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
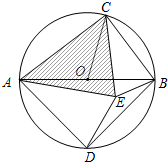 若在⊙O内存在点E,使AE=AD,CB=CE.
若在⊙O内存在点E,使AE=AD,CB=CE.查看答案和解析>>
科目:初中数学 来源:2012年浙江省杭州市中考数学模拟试卷(二)(解析版) 题型:解答题
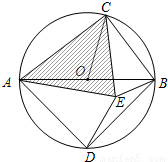
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com