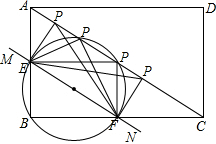
解:(1)能.以EF为直径作圆,圆与AC的交点就是P点,P点位置如图所示:
∴共有4个:①∠PEF=90°;②∠PFE=90°;③∠EPF=90°(两种);
(2)在矩形ABCD中
∵AB=3,BC=4,
∴AC=5.
∵S
△ABC=

•BC•AB,
∴S
△ABC=6.
∵FC=x,
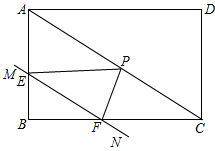
∴BF=4-x.
在△ABC中
∵EF∥AC,
∴△BEF∽△BAC.
∴
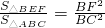
.
∴
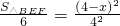
.
∴S
△BEF=6×
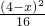
=

(x-4)
2.
∵PA=PC,EF∥AC,
∴S
△AEP=S
△CPF=

FC•CP•sin∠ACB.
∵sin∠ACB=

,
∴S
△AEP=

×

x×

=

x.
∴S
△PEF=S
△ABC-(S
△BEF+S
△AEP+S
△CFP)
=6-[

(x-4)
2+

x+

x]
=-

x
2+

x(0<x<4).
分析:(1)共有四个:①∠PEF=90°;②∠PFE=90°;③∠EPF=90°(两种),此种情况,可以EF为直径作圆,圆与AC的交点就是P点.
(2)由于三角形PEF的面积无法直接求出,可用三角形ABC的面积减去三角形AEP、BEF、CFP三个小三角形的和来求.
三角形BEF的面积可用三角形ABC的面积和它们的相似比来求出.
由于P是AC中点,而MN∥AC,根据等底等高的三角形面积相等可得出三角形AEP和CPF的面积相等,因此只需求出三角形FCP的面积即可.三角形PCF中,CF的长已知了为x,CF边上的高可用PC的长和∠ACB的正弦值求出.
由此可得出三角形PEF的面积S与x的函数关系式.
点评:本题主要考查了矩形的性质、图形面积的求法以及二次函数的应用等知识点.


 解:(1)能.以EF为直径作圆,圆与AC的交点就是P点,P点位置如图所示:
解:(1)能.以EF为直径作圆,圆与AC的交点就是P点,P点位置如图所示: •BC•AB,
•BC•AB,
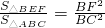 .
.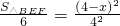 .
.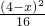 =
= (x-4)2.
(x-4)2. FC•CP•sin∠ACB.
FC•CP•sin∠ACB. ,
, ×
× x×
x× =
= x.
x. (x-4)2+
(x-4)2+ x+
x+ x]
x] x2+
x2+ x(0<x<4).
x(0<x<4).

 阅读快车系列答案
阅读快车系列答案
