
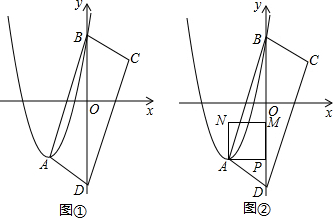
分析 (1)根据配方法,可得顶点坐标,根据自变量与函数值得对应关系,可得B点坐标,
(2)根据B点的纵坐标小于零,可得不等式,根据解不等式,可得答案;
(3)根据平行四边形的性质,可得答案;
(4)根据正方形的边长小于BP,可得不等式,根据解不等式,可得答案.
解答 解:(1)配方,得
y=(x-m)2+$\frac{4}{3}$m,顶点A的坐标为(m,$\frac{4}{3}$m)
当x=0时,y=m2+$\frac{4}{3}$m,B点坐标为(0,m2+$\frac{4}{3}$m)
(2)点B能落在y轴负半轴上,理由如下:
由顶点坐标,得m<0,
B点的纵坐标小于零,得
m2+$\frac{4}{3}$m=m(m+$\frac{4}{3}$)<0,
由m<0,得
m+$\frac{4}{3}$>0,
得-$\frac{4}{3}$<m<0,
当-$\frac{4}{3}$<m<0时,点B能落在y轴负半轴上;
(3)OB=m2+$\frac{4}{3}$m,OA=-$\frac{5}{3}$m,
l=AC+BD=2OB+2OA=2(m2+$\frac{4}{3}$m)+2×(-$\frac{5}{3}$m)
即l=2m2-$\frac{2}{3}$m;
(4)由题意,得
AP<BP,
即-m<m2+$\frac{4}{3}$m-$\frac{4}{3}$m
解得m(m+1)>0,
由m<0,得m>-1,
当-1<m<0时,AP<BP,
正方形APMN与四边形ABCD重叠部分图形为四边形时,m的范围是-1<m<0.
点评 本题考查了二次函数综合题,解(1)的关键是配方法;解(2)的关键是解不等式;解(3)的关键是利用平行四边形的性质得出AC+BD=2OB+2OA;解(4)的关键是由四边形得出AP<BP.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{y}{2}-\frac{1}{4y}-3=0$ | B. | $2y-\frac{1}{4y}-3=0$ | C. | $2y-\frac{4}{y}-3=0$ | D. | $\frac{y}{2}-\frac{4}{y}-3=0$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com