Question

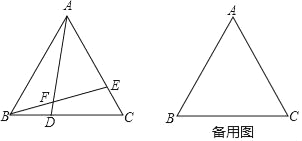
【题目】（1）如图，在等边三角形ABC的边BC、AC上分别取点D、E，使得BD=CE，AD与BE相交于点F．求∠AFE的度数．

（2）若点D、E分别在边CB、AC的延长线上，同样BD=CE，AD与BE所在直线相交于点F．请你先画出图形，再求出∠AFE的度数．

Answer 1

【答案】（1）∠AFE=60°；（2）画图见解析，∠AFE=60°．

【解析】整体分析：

(1)先用SAS证明△ABD≌△BCE，结合三角形的外角的性质即可求得∠AFE的度数；(2)根据题意画出图形，求AFE的度数的方法与(1)类似.

解：(1)∵△ABC为等边三角形，

∴AB=BC，∠ABC=∠C=60°．

在△ABD和△BCE中，

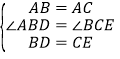
∴△ABD≌△BCE，

∴∠BAD=∠CBE．

又∵∠AFE=∠ABF+∠BAD=∠ABC

∴∠AFE=60°．

(2)如图．

∵△ABC为等边三角形，

∴AC=BC，∠ABC=∠ACB=60°．

∴∠ABD=∠BCE=120°，

∵BD=CE，

在△ABD和△BCE中，

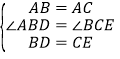
∴△ABD≌△BCE，

∴∠DAB=∠CDE，

∵∠ABE=∠AFB+∠FAB=∠ABC+∠CBE，

∴∠AFB=∠ABC=60°，

∴∠AFE=60°．