
 小明家、学校、书店在同-条马路上,请你用学过的数学知识在图中标明它们三者间的距离.小明的步行速度是5千米/时,小明中午11:30放学,下午1:30上课,吃饭要用30分钟,中午他要到书店买完书再到学校上课,选书时间是10分钟.请你帮小明计算一下,他吃完中午饭最晚什么时间从家出发上课才不会迟到?
小明家、学校、书店在同-条马路上,请你用学过的数学知识在图中标明它们三者间的距离.小明的步行速度是5千米/时,小明中午11:30放学,下午1:30上课,吃饭要用30分钟,中午他要到书店买完书再到学校上课,选书时间是10分钟.请你帮小明计算一下,他吃完中午饭最晚什么时间从家出发上课才不会迟到? 分析 先通过他中午放学到下午上课之间的时间,再分别减去吃饭要用30分钟、选书时间是10分钟,可列出二元一次不等式,再估算出解,就可以求得他去书店和到学校走路所用时间,由此可算出他在什么时间出发不会迟到.
解答 解:设小明家到学校为x千米,学校到书店y千米,
小明中午11:30放学,下午1:30上课,吃饭要用30分钟,选书时间是10分钟
那么他剩余的时间为:(2-0.5-$\frac{1}{6}$)=$\frac{4}{3}$(小时),
要使他上课不迟到,则需他走路所用的时间少于$\frac{4}{3}$小时,
已知小明步行速度是5千米/小时,故由题意可列出二元一次不等式:
(2x+2y)÷5<$\frac{4}{3}$,
x+y<$\frac{10}{3}$≈3.3,
故可由此标出它们三者间的距离分别为:小明家到学校为1千米,学校到书店0.5千米;
去书店和到学校走路所用时间为:(x+2y)÷5=0.4(小时)=24(分钟),
在书店买书的时间为10分钟,
总共耽误的时间为34分钟,
故他需要在12:56前出发,上课才能不迟到.
点评 本题考查了列二元一次方程和估算它的解以及有理数的混合运算的运用,正确得出总路程的取值范围是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一个坡角为30°的斜坡上有一棵树,高为AB,当太阳光与水平面75°角时.测得该树坡上的树影BC的长为4($\sqrt{3}-1$)米.求树高.
如图,在一个坡角为30°的斜坡上有一棵树,高为AB,当太阳光与水平面75°角时.测得该树坡上的树影BC的长为4($\sqrt{3}-1$)米.求树高.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
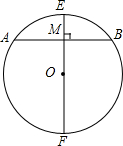 如图所示,M为⊙0内任一不与点O重合的点,连接0M,AB为过M点且与0M垂直的一条弦,EF为过M点的一条直径,求证:在过M点的所有弦中,AB是最短的一条,EF是最长的一条.
如图所示,M为⊙0内任一不与点O重合的点,连接0M,AB为过M点且与0M垂直的一条弦,EF为过M点的一条直径,求证:在过M点的所有弦中,AB是最短的一条,EF是最长的一条.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com