
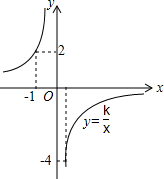
 反比例函数y=$\frac{k}{x}$的图象如图所示,根据图中的信息可得到不等式组$\left\{\begin{array}{l}{\frac{k}{x}≥-4}\\{\frac{k}{x}<2}\end{array}\right.$的解集为( )
反比例函数y=$\frac{k}{x}$的图象如图所示,根据图中的信息可得到不等式组$\left\{\begin{array}{l}{\frac{k}{x}≥-4}\\{\frac{k}{x}<2}\end{array}\right.$的解集为( )| A. | -4≤x<0或0<x<2 | B. | x<-1或x≥$\frac{1}{2}$ | C. | -1<x≤$\frac{1}{2}$ | D. | -1<x<0或0<x≤$\frac{1}{2}$ |
分析 由图象知:反比例函数y=$\frac{k}{x}$的图象过点(-1,2),求得反比例函数的解析式,根据图象即可求出结果.
解答 解:由图象知:反比例函数y=$\frac{k}{x}$的图象过点(-1,2),
∴k=-2,∴反比例函数的解析式为:y=$\frac{-2}{x}$,
当y=-4时,x=-$\frac{1}{2}$,
∴不等式组$\left\{\begin{array}{l}{\frac{k}{x}≥-4}\\{\frac{k}{x}<2}\end{array}\right.$的解集为x<-1,或x≥-$\frac{1}{2}$,
故选B.
点评 题考查了反比例函数的性质.对于反比例函数y=$\frac{k}{x}$,当k>0时,在每一个象限内,函数值y随自变量x的增大而减小;当k<0时,在每一个象限内,函数值y随自变量x增大而增大.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
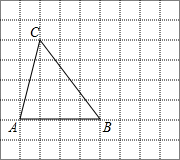 作图题:在方格纸中,将△ABC向右平移4个单位得到△A1B1C1
作图题:在方格纸中,将△ABC向右平移4个单位得到△A1B1C1查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{8}$-2$\sqrt{2}$=0 | C. | $\sqrt{24}$÷$\sqrt{6}$=4 | D. | (2-$\sqrt{5}$)(2+$\sqrt{5}$)=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com