
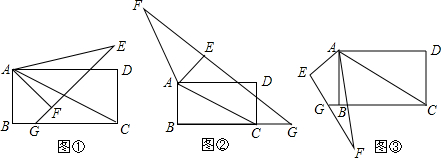
分析 图②结论:EG=EF+CG,如图2,连接AG,证明Rt△ABG≌Rt△AEG,问题即可得证;图③结论:EG=CG-EF,连接AG,证明Rt△ABG≌Rt△AEG,问题即可得证.
解答 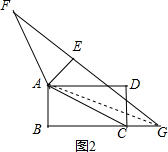 解:猜想:图②结论:EG=EF+CG,
解:猜想:图②结论:EG=EF+CG,
图③结论:EG=CG-EF,
证明图②,如图2,连接AG,
∵将△ABC绕点A旋转得到△AEF,
∴AB=AE,∠FEA=∠GEA=∠B=90°,
在Rt△ABG和Rt△AEG中,
$\left\{\begin{array}{l}{AB=AE}\\{AG=AG}\end{array}\right.$,
∴Rt△ABG≌Rt△AEG,
∴BG=EG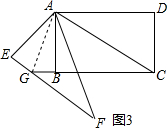
又∵BC=EF,BG=BC+CG
∴EG=EF+CG;
证明图③,如图3,连接AG,
同理可证:Rt△ABG≌Rt△AEG,
∴BG=EG,
又∵BC=EF,BG=CG-BC,
∴EG=CG-EF.
点评 本题考查了全等三角形的判定和性质,旋转的性质,正确的作出辅助线,构造全等三角形是解题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
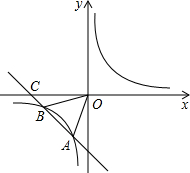 在平面直角坐标系xOy中,O是坐标原点;一次函数y=kx+b(k≠0)图象与反比例函数y=$\frac{m}{x}({m≠0})$的图象交于A(a,2a-1)、B(3a,a).
在平面直角坐标系xOy中,O是坐标原点;一次函数y=kx+b(k≠0)图象与反比例函数y=$\frac{m}{x}({m≠0})$的图象交于A(a,2a-1)、B(3a,a).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
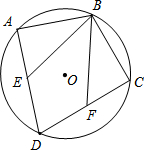 如图,四边形ABCD是⊙O的内接四边形,$\widehat{AB}$=$\widehat{BC}$,点E、F分别是弦AD、DC上的点.
如图,四边形ABCD是⊙O的内接四边形,$\widehat{AB}$=$\widehat{BC}$,点E、F分别是弦AD、DC上的点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
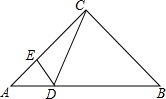 如图,在△ABC中(BC>AC),∠ACB=90°,点D在AB边上,DE⊥AC于点E.
如图,在△ABC中(BC>AC),∠ACB=90°,点D在AB边上,DE⊥AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
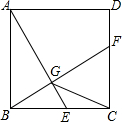 如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为$\sqrt{5}$-1.其中正确的说法是②④.(把你认为正确的说法的序号都填上)
如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为$\sqrt{5}$-1.其中正确的说法是②④.(把你认为正确的说法的序号都填上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com