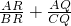练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    设M、N分别是△ABC两边AB、AC的中点，P是MN上任意一点，延长BP交AC于点Q，延长CP交AB于R，则数学公式=________．

    1
    分析：由三角形的中位线定理可得MN∥BC且=，△RMP∽△RBC，△QPN∽△QBC，利用相似三角形的对应线段成比例进行转化．
    解答：解：如图，∵M、N为AB、AC边的中点，
    ∴AM=BM，AN=NC，MN∥BC且=，△RMP∽△RBC，△QPN∽△QBC，
    ∴=（-1）+（-1）+2
    =++2
    =2-2（+）
    =2-2（+）
    =2-2•=2-2×=1．
    故本题答案为：1．
    点评：本题主要考查了三角形的中位线定理，相似三角形的判定与性质．关键是利用了线段之间的转化，相似比的转化解题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

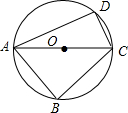    精英家教网四边形ABCD内接于圆，已知∠ADC=90°，CD=4，AC=8，AB=BC．设O是AC的中点．
    （1）设P是AB上的动点，求OP+PC的最小值；
    （2）设Q，R分别是AB，AD上的动点，求△CQR的周长的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    27、已知，如图，AB∥CD．设M、N分别是AB和CD上的动点，P为平面上任一点（不在直线AB、CD上），PM⊥PN．试在所给的图形中，探究∠AMP与∠CNP之间的关系．

    查看答案和解析>>

    科目：初中数学 来源：期末题 题型：探究题

    已知，如图，AB∥CD．设M、N分别是AB和CD上的动点，P为平面上任一点（不在直线AB、CD上），PM⊥PN．试在所给的图形中，探究∠AMP与∠CNP之间的关系．

    查看答案和解析>>

    科目：初中数学 来源：期末题 题型：解答题

    已知，如图，AB∥CD，设M、N分别是AB、CD上的动点，P为平面上任一点（不在直线AB、CD上），PM⊥PN。试在所给的图形中，探究∠AMP与∠CNP之间的关系。

    查看答案和解析>>

    科目：初中数学 来源：2008年安徽省马鞍山市第二中学理科实验班招生数学试卷（解析版） 题型：解答题

    四边形ABCD内接于圆，已知∠ADC=90°，CD=4，AC=8，AB=BC．设O是AC的中点．
    （1）设P是AB上的动点，求OP+PC的最小值；
    （2）设Q，R分别是AB，AD上的动点，求△CQR的周长的最小值．

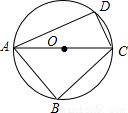
    查看答案和解析>>

    同步练习册答案