
 如图,BD为⊙O的直径,A为
如图,BD为⊙O的直径,A为 的中点,A交BC于点E,过D作⊙O的切线,交BC的延长线于F,
的中点,A交BC于点E,过D作⊙O的切线,交BC的延长线于F,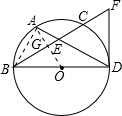 解:(1)连接OA,
解:(1)连接OA, 的中点,
的中点, =
= ,即AB2=AE•AD=2×(2+4)=12,
,即AB2=AE•AD=2×(2+4)=12, .
.

科目:初中数学 来源: 题型:
 10、如图,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.小明用这些数据很快算出了电线杆AB的高.请你计算,电线杆AB的高为( )
10、如图,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.小明用这些数据很快算出了电线杆AB的高.请你计算,电线杆AB的高为( )查看答案和解析>>
科目:初中数学 来源: 题型:
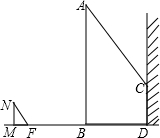 如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
(2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源:2011届江苏省九年级下册《投影与视图》单元测试数学卷 题型:选择题
如图,一电线杆AB的影子分别落在地上和墙上,某一时刻,小明竖起1m高的直杆,量
得其影长为0.5m,此时,他又量得电线杆AB落在地上的影子BD长3m,落在墙上的影子
CD的高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为
( )
A.5m B.6m C.7m D.8m

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com