
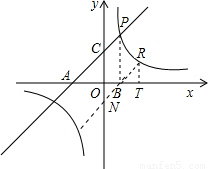
 分别交x轴、y轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.
分别交x轴、y轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9. ,用a表示AB,PB,根据S△ABP=9可以求出a,从而求出P的坐标;
,用a表示AB,PB,根据S△ABP=9可以求出a,从而求出P的坐标; ,利用BR∥AP可以得到△AOC∽△BTR,再利用相似三角形的性质-对应边成比例可以得到关于b的方程,解方程求出b,也就求出了R的坐标.
,利用BR∥AP可以得到△AOC∽△BTR,再利用相似三角形的性质-对应边成比例可以得到关于b的方程,解方程求出b,也就求出了R的坐标. 解:(1)∵直线
解:(1)∵直线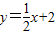 分别交x轴、y轴于A、C
分别交x轴、y轴于A、C .即:AB=4+a,PB=
.即:AB=4+a,PB=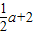
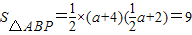
 ,
,
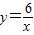 ,
, ,
,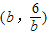 ,即:BT=b-2,
,即:BT=b-2,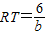 ,
,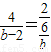 ,
,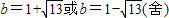 ,
, ,
, ).
). ,
, ).
).

科目:初中数学 来源:2003年全国中考数学试题汇编《反比例函数》(03)(解析版) 题型:解答题
 分别交x轴、y轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.
分别交x轴、y轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《一次函数》(04)(解析版) 题型:解答题
 与x轴、y轴分别交于A、B两点,圆M经过原点及A、B两点.
与x轴、y轴分别交于A、B两点,圆M经过原点及A、B两点.
查看答案和解析>>
科目:初中数学 来源:2009年浙江省杭州市萧山区中考模拟数学试卷(万向初中 庄国军)(解析版) 题型:解答题
 分别交x轴、y轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.
分别交x轴、y轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.查看答案和解析>>
科目:初中数学 来源:2003年湖北省荆州市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com